|
Où se trouve le centre de la France ?
En me baladant sur le net, j'ai vu que plusieurs localités différentes
revendiquaient être le "centre" géographique de la France. En revanche, je
n'ai pas trouvé d'explications sur la méthode qui avait été utilisée dans chaque
cas
pour aboutir
à la conclusion. Je n'ai pas trouvé non plus la définition du mot "centre"
dans ce cas précis.
J'ai donc décidé d'apporter ma petite pierre à cet édifice,
de la façon la plus rigoureuse possible. Tout d'abord, en donnant la définition
du mot "centre" que j'ai utilisée (celle qui, pour moi, s'approche le plus
de la définition du centre d'un cercle) : le centre d'une figure
géométrique est un point (avec cette définition, il
pourrait y en avoir plusieurs) qui
est "le plus équidistant possible" de tous les points de cette figure.
L'expression "le plus équidistant possible" a l'air vague. Il n'en est rien
: je veux dire
qu'un point sera un centre si les distances de ce point à tous les points
de la frontière sont le moins possible différentes. Autrement dit, si ces
distances sont dispersées au minimum. Et enfin, dit mathématiquement, si la
variance de l'ensemble de ces distances est minimum.
Ensuite, j'ai écrit un petit programme en pascal (Delphi)
qui cherche ces points. Les connaisseurs (!) trouveront le code de ce programme
au bas de la page. Il utilise l'image monochrome (le point rouge
a été ajouté après) ci dessous :
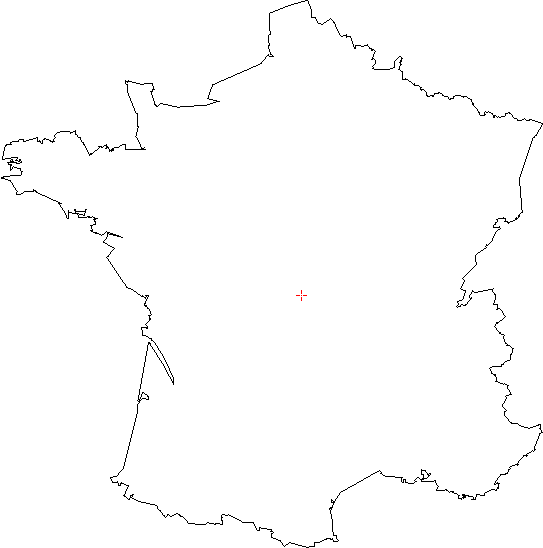
Cette image fait 543 pixels de large et 548 pixels de haut. Il y a donc au
total 543x548=297564 points dans l'image. La frontière est constituée de 4029
points noirs.
Pour chaque point de l'image non situé sur la frontière (293535 points), le
programme calcule la distance de ce point à chacun des 4029 points constituant
la frontière (ça fait un paquet de calculs !). Ensuite, le programme calcule
la variance des distances du point choisi à chaque point de la frontière, et
mémorise cette variance. Enfin, le programme cherche la variance minimum et
les points qui correspondent.
Le verdict : il n'y a qu'un seul point répondant à la
question. C'est le point marqué en rouge sur la carte. Il se trouve à 301 pixels
du bord gauche et à
295 pixels du bord supérieur.
Je vais maintenant déterminer précisément quel est ce lieu.
Pour cela, j'ai utilisé le site Lion1906,
qui permet de déterminer les coordonnées de toutes les localités de France.
Les coordonnées angulaires utilisées sont
toutes exprimées en radians.
Le point le plus au nord de la carte (ordonnée nulle)
est
Bray-Dunes (latitude N : 0,891703259).
Le point le plus à l'est de la carte (abscisse 543) est l'embouchure
de la Lauter (longitude
E : 0,140145087).
Le point le plus au sud de la carte (ordonnée 548) est Prats de
Mollo (latitude N : 0,73885605).
Le point le plus à l'ouest de la carte (abscisse nulle) est la
pointe de Corsen (longitude
O
: 0,0837128).
(sources : Quid)
En faisant un simple changement de repère, on calcule que
les coordonnées angulaires du point (301;295) de ma carte sont (301x(0,140145087-(-0,0837128))/543-0,0837128;295x(0,73885605-0,891703259)/548+0,891703259),
c'est à dire :
Longitude Est : 0,040377852
Latitude Nord : 0,809422371
A nouveau, le site Lion1906 nous
donne la liste des localités les plus proches de ce point :
| Palmarès (!) |
Ville |
Code postal |
Distance au point théorique |
| 1 |
Saint Sauvier |
03370 |
1.7 Km |
| 2 |
Leyrat
|
23600 |
2.6 Km |
| 3 |
Treignat
|
03380 |
3.3 Km |
| 4 |
Saint Pierre le Bost
|
23600 |
4.4 Km |
| 5 |
Boussac Bourg
|
23600 |
6.2 Km |
| 6 |
Saint Palais
|
03370 |
6.4 Km |
| 7 |
Mesples
|
03370 |
6.9 Km |
| 8 |
Lavaufranche
|
23600 |
7.6 Km |
| 9 |
Saint Marien
|
23600 |
7.6 Km |
| 10 |
Saint Silvain Bas le Roc
|
23600 |
7.8 Km |
And the winner is...
Saint-Sauvier !
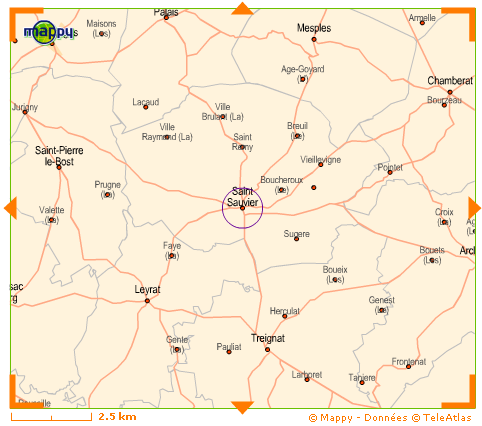
Vous saurez tout sur ce charmant petit village de l'Allier
(377 habitants) en tapant "Saint-Sauvier" dans Google (1260 réponses
en français
au 11/02/04, quand
même !).
|
Generated with HyperDelphi
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls, StdCtrls, Grids;
type
TForm1 = class(TForm)
Image1: TImage;
Button1: TButton;
Grille: TStringGrid;
Memo1: TMemo;
procedure Button1Click(Sender: TObject);
private
{ Déclarations privées }
Function getpixel(ax,ay : integer): TColor;
public
{ Déclarations publiques }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
type
TRGBArray = ARRAY[0..0] OF TRGBTriple; // élément de bitmap (API windows)
pRGBArray = ^TRGBArray; // type pointeur vers tableau 3 octets 24 bits
var
// attention, pas de bitmap plus haut que 2048 lignes
Lignes : array[0..2047] of pRGBArray;
function distance(a,b:TPoint):real; {carré de la distance AB}
begin
result:=sqr(a.x-b.x)+sqr(a.y-b.y);
end;
// Accès rapide à un pixel
Function Tform1.getpixel(ax,ay : integer): TColor;
const
Filler : array[0..2] of byte = (0,0,0); // noir par défaut
var interm:TRGBTRiple; R,G,B : integer;
begin
if (ax >= 0) AND (ay >= 0) AND // limites
(ax < Image1.Picture.Bitmap.width-1) AND (ay < Image1.Picture.Bitmap.height-1) then
interm := Lignes[ay,ax]
else
interm := Trgbtriple(Filler); // transtypage des 3 bytes
R := interm.RGBtRed;
G := interm.RGBtGreen;
B := interm.RGBtBlue;
result:= RGB(R,G,B);
end;
procedure TForm1.Button1Click(Sender: TObject);
var x,y,fx,fy,nbpoints,count:integer; d,sd,sd2,v,ppv:real;
begin
Screen.Cursor:=crHourGlass;
Grille.RowCount:=Image1.Picture.Bitmap.height*Image1.Picture.Bitmap.width;
Image1.Picture.Bitmap.pixelformat := pf24bit;
// précalcul des scanline
For y := 0 to Image1.Picture.Bitmap.height-1 do Lignes[y] := Image1.Picture.Bitmap.scanline[y];
count:=0;
// pour chaque point de l'image
for y:=0 to Image1.Picture.Height-1 do
for x:=0 to Image1.Picture.Width-1 do begin
// (inutile si c'est un point de la frontière)
if (getpixel(x,y)=clWhite) then begin
Caption:=IntToStr(x)+' - '+IntToStr(y);
nbpoints:=0; sd:=0; sd2:=0;
// pour chaque point de la frontière :
// (pour gagner du temps, on aurait pu chercher les points de la
// frontière et les mettre dans un tableau avant cette boucle)
for fy:=0 to Image1.Picture.Height-1 do
for fx:=0 to Image1.Picture.Width-1 do
if (getpixel(fx,fy)=clBlack) then begin
inc(nbpoints);
d:=distance(Point(x,y),Point(fx,fy));
sd:=sd+d; // somme des distances
sd2:=sd2+d*d; // somme des carrés des distances
end;
v:=sd2/nbpoints-(sd/nbpoints)*(sd/nbpoints); // variance
// on stocke le point et sa variance dans le tableau
Grille.Cells[0,count]:=IntToStr(x);
Grille.Cells[1,count]:=IntToStr(y);
Grille.Cells[2,count]:=FloatToStr(v);
inc(count);
end;
end;
// on cherche la plus petite variance.
ppv:=StrToFloat(Grille.Cells[2,0]);
for y:=0 to count-1 do
if StrToFloat(Grille.Cells[2,y])<ppv then ppv:=StrToFloat(Grille.Cells[2,y]);
// on énumère tous les points qui ont la plus petite variance
Memo1.Clear;
for y:=0 to count-1 do
if Grille.Cells[2,y]=FloatToStr(ppv) then begin
memo1.Lines.Add(Grille.Cells[0,y]+#9+Grille.Cells[1,y]);
Image1.Picture.Bitmap.Canvas.Pixels[StrToInt(Grille.Cells[0,y]),StrToInt(Grille.Cells[1,y])]:=clRed;
end;
Screen.Cursor:=crDefault;
end;
end.
|
|