Les arbres n-aires : codage d'un dictionnaire

Nous allons étudier dans ce Chapitre la façon de coder un dictionnaire dans un arbre n-aire (chaque noeud de l'arbre possède n branches).

Structure des données

Pour commencer, nous allons étudier la structure d'un noeud. On suppose que le dictionnaire est en majuscules, c'est pourquoi nous n'avons que 26 lettres possibles pour un noeud. Bien évidemment, cette structure peut être élargie si on veut aussi prendre en compte les minuscules et les chiffres ou autres signes. Nous voulons aussi afficher l'arbre n-aire à l'écran (sur un exemple comportant seulement quelques mots), ce qui implique que chaque noeud aura une position à l'écran, matérialisée par deux coordonnées x et y. Chaque noeud contient une lettre, donc une variable de type char, et il doit contenir aussi un indicateur boolean utilisé pour indiquer si un mot est entier : par exemple, supposons qu'on code le mot "CARTE" dans un arbre; l'arbre aura donc 5 niveaux. La dernière lettre du mot (le "E") aura son indicateur boolean positionné à true. Par contre, la lettre "A" n'aura pas son indicateur positionné, car le mot "CA" n'est pas un mot du dictionnaire. La lettre "R" aura son indicateur positionné, car le mot "CAR" fait partie du dictionnaire de la langue française.

Un noeud possède donc:

- 26 fils, les lettres possibles de 'A' à 'Z'

- les coordonnées (x,y) qui seront utilisées pour l'affichage graphique de l'arbre

- une lettre

- un indicateur boolean

Noeud =
 class
private
 Fils: array['A'..'Z'] of Noeud; //liste de fils
 x, y: integer; // pour dessin arbre
 Lettre: char; // lettre contenue dans ce noeud de l'arbre
 Entier: boolean; //flag indiquant si le mot est entier
public
 constructor create;
 destructor destroy;
end; { Noeud }
 

Etudions maintenant la structure d'un arbre. Comme nous l'avons déjà vu, un arbre est constitué par sa tête, et par une autre variable nous permettant de parcourir l'arbre. Les opérations relatives à un arbre sont les suivantes :

- ajout d'un mot

- chargement d'un fichier dans l'arbre en utilisant l'opération d'ajout

- compter le nombre de noeuds terminaux se trouvant en-dessous d'un noeud quelconque

- l'affichage graphique et l'affichage texte (création d'une liste de mots du dictionnaire)

- recherche d'un mot

Dans notre exemple, nous avons choisi une liste de 13 mots de 5 lettres chacun. A l'aide de la fonction qui compte le nombre de noeuds terminaux, on peut donc dire combien de mots comporte l'arbre.

//arbre d'ordre 26
Arbre =
 class
private
 tete, courant: noeud;
public
 constructor create;
 destructor destroy; override;
 procedure rajouter_mot(LeMot: string);
 procedure charger(NomFic: string);
 procedure Affiche(S, prefixe: string);
 procedure dessine(en_cours: noeud; limg, old_x, old_y: integer);
 function Trouve(LeMot: string): boolean;
 function compter_terminaux(en_cours: noeud): integer;
end;
 

Nous allons voir, une par une, toutes les procédures décrites ci-dessus. Mais auparavant, voici un exemple concret d'arbre n-aire qui contient des mots de longueur 3 (EMU,EPI), de longueur 4 (EMUE, EMIS, EMET, EPIE, PRIS) et de longueur 5 (EPIER, EPRIS), dont l'indicateur est positionné à true, et qui est représenté sur ce schéma par un petit triangle noir dans le coin des cases en bas à droite.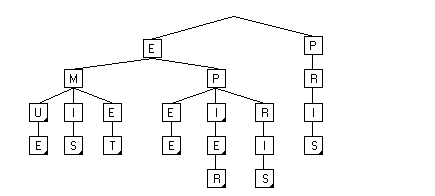

La procédure d'ajout d'un mot

On part du sommet de l'arbre. La procédure est récursive, et comme toute procédure récursive, elle a un point d'appui (ou d'arrêt). On va ajouter le mot dans l'arbre lettre par lettre, en descendant dans l'arbre d'un niveau à chaque lettre. Le mot est donc "mangé" progressivement du début vers la fin.

1) Le point d'arrêt est atteint quand on n'a plus de lettres à ajouter dans l'arbre. Dans ce cas, on positionne le noeud courant à true, pour indiquer que c'est un mot complet et on quitte la procédure.

2) On a encore des lettres à ajouter dans l'arbre. Prenons le cas du mot "EPI". On est au sommet de l'arbre. Si la lettre "E" existe déjà dans l'arbre en tant que noeud fils du sommet, alors :

- on "mange" le "E"; le mot à rajouter devient "PI" mais il faut le mettre sous le "E"

- on descend sur le fils "E"

- on rajoute (récursivement) le mot "PI"

Si la lettre "E" n'existe pas, alors :

- on crée le noeud fils "E"

- on exécute les étapes ci-dessus.

Voici le programme correspondant :

procedure arbre.rajouter_mot(LeMot: string);
var lettre: char;
begin
 if LeMot = '' then
 begin
 courant.entier := true;
 exit;
 end;
 lettre := LeMot[1];
 if courant.fils[lettre] <> nil then // si la lettre existe déjà
 courant := courant.fils[lettre] // alors on se positionne sur la lettre suivante
 else // sinon il faut créer cette lettre dans l'arbre
 begin
 courant.fils[lettre] := noeud.create;
 courant := courant.fils[lettre];
 courant.lettre := lettre; // la lettre est maintenant dans l'arbre
 end;
 delete(LeMot, 1, 1); // on efface la lettre du mot puisqu'elle est déjà dans l'arbre
 rajouter_mot(LeMot); // et on rajoute le reste
end;
 

La procédure de chargement d'un fichier

Le fichier étant un simple fichier texte, il suffit de le lire ligne par ligne et d'ajouter au fur et à mesure les mots lus dans l'arbre.

procedure arbre.charger(NomFic: string);
var s: string;
 chemin: string; // le chemin de l'appli, AVEC l'antislash final
 f: textfile;
begin
 chemin := ExtractFilePath(Application.ExeName);
 assignFile(f, chemin + nomFic);
 reset(f);
 repeat
 readln(f, s);
 courant := tete; // on se positionne en tête de l'arbre
 rajouter_mot(s); // et on rajoute le mot
 until eof(f);
 closeFile(f);
end;
 

Comptage des noeuds terminaux

Pour dessiner un arbre, nous avons besoin de cette fonction. En effet, si un père a deux noeuds terminaux, sa position à l'écran sera au milieu de ses deux fils (il s'agit de la position sur l'axe des abscisses, les "x"; en tant que père il sera positionné au dessus de ses fils sur l'axe des ordonnées, les "y"). Cela est valable aussi pour un père qui n'a pas directement de noeuds terminaux, mais dont les fils ou sous-fils en ont. Il faut donc parcourir récursivement le sous-arbre dont le père est le noeud courant pour arriver jusqu'aux noeuds terminaux.

Une solution serait la suivante :

- la somme des noeuds terminaux ayant pour ancêtre un noeud donné est :

- égale à un si le noeud en question n'a pas de fils (point d'arrêt)

- égale à la somme des noeuds terminaux de ses fils sinon

Mais, dans ce cas, on peut supprimer le point d'arrêt et faire fusionner les deux conditions. En effet, on n'a qu'à parcourir tous les fils du noeud en cours et, s'ils ne sont pas égaux à nil, incrémenter alors une variable locale avec leurs propres noeuds terminaux. Si, à la fin, le total obtenu est égal à zéro, alors aucun des fils du noeud en cours n'existe (point d'arrêt de la récursivité) donc on initialise la variable locale à 1 et on sort.

function arbre.compter_terminaux(en_cours: noeud): integer;
var i: char;
 total: integer;
begin
 total := 0;
 for i := 'A' to 'Z' do
 if en_cours.fils[i] <> nil then
  inc(total, compter_terminaux(en_cours.fils[i]));
 if total = 0 then inc(total);
 compter_terminaux := total;
end;
 

Affichage graphique d'un arbre n-aire

La procédure d'affichage d'un arbre nécessite, pour commencer, une image et ensuite quelques petits calculs mathématiques, ainsi que le nombre total de noeuds terminaux qui se trouvent en-dessous du noeud courant. La première chose à faire est de compter le nombre de noeuds terminaux dérivant du noeud en cours, afin de décider où il sera placé graphiquement, ceci nous amenant donc au calcul de ses coordonnées. Ensuite pour chaque noeud dessiné, on doit tracer une ligne le reliant à son père, ce qui nous amène à l'utilisation de 2 paramètres (old_x,old_y) de type integer. On suppose que chaque noeud occupe 50 pixels en largeur et 80 en hauteur. Ainsi, si un noeud a 4 fils, sa position sera à la moitié de 4*50, soit " (4*50) div 2". S'il n'a que 2 fils, il sera à " (2*50) div 2". Mais comment faire pour que les noeuds d'un même niveau se décalent vers la droite ? En effet dans le dessin suivant, au niveau 1, nous avons deux fils, le premier ayant 2 fils terminaux et le deuxième trois fils terminaux.

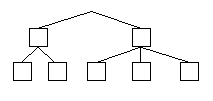
Si on applique la formule ci-dessus, alors le premier noeud du niveau 1 est situé à "x:=(2*50)/2" (soit x=50) et le deuxième est situé à "x:=(3*50)/2" (soit x=75). On constate alors que ces deux noeuds se chevauchent, puisque le premier est situé à x=50 et il occupe 50 pixels (jusqu'à cent; or le deuxième est situé à x=75). Donc, à chaque dessin d'une partie de l'arbre, il faut voir quelle est la largeur qu'il requiert et la passer en paramètre à ses frères, de façon à ce que ceux-ci commencent leur dessin avec un décalage vers la gauche. Ainsi dans l'exemple ci-dessus, le premier noeud nécessite 100 pixels (car il a deux fils terminaux, qui seront dessinés à partir de la position 0 ), et le deuxième noeud nécessite 150 pixels (car il a trois noeuds terminaux, qui seront dessinés à partir de la position 100). Ceci nous amène à un nouveau paramètre, appelé "limg" qui indique la position à partir de laquelle on doit dessiner le sous arbre du noeud en cours. On effectue ensuite les opérations suivantes :

- on calcule la position du noeud en cours (x et y)

- on relie ce noeud à son père

- on parcourt tous ses fils et pour chaque fils non vide on dessine le sous-arbre correspondant en faisant un appel récursif.

procedure arbre.dessine(en_cours: noeud; limg, old_x, old_y: integer);
var x, y, nb: integer;
 i: char;
begin
//nb:=compter_terminaux(courant); // effet joli
 nb := compter_terminaux(en_cours);
 x := limg + (50 * nb) div 2;
 y := old_y + 80;
 if en_cours <> tete then
 with form1.image1.picture.bitmap.canvas do
 begin
 textout(x, y, en_cours.lettre);
 en_cours.x := x; en_cours.y := y;
 moveto(x, y - 5); lineto(old_x, old_y);
 end;
 for i := 'A' to 'Z' do
 if en_cours.fils[i] <> nil then
 begin
 nb := compter_terminaux(en_cours.fils[i]);
 dessine(en_cours.fils[i], limg, x, y + 20);
 limg := limg + nb * 50;
 end;
end;
 

Affichage de texte (création d'une liste de mots du dictionnaire)

Pour réaliser un affichage de tous les mots de l'arbre, on n'a qu'à parcourir ses noeuds et quand on arrive à un noeud dont l'indicateur boolean est positionné, on ajoute le mot à une liste. Ensuite, on parcourt tous les fils du noeud en cours en faisant un appel récursif. Comme les mots se constituent au fur et à mesure qu'on descend dans l'arbre, on utilise un paramètre à cet effet.

procedure arbre.Affiche(S: string);
var i: char;
 aux: noeud;
begin
 if courant.Entier then Form1.Memo1.Lines.Add(s);
 for i := 'A' to 'Z' do
 if courant.fils[i] <> nil then
 begin
 aux := courant;
 courant := courant.fils[i];
 Affiche(S + i);
 courant := aux;
 end;
end;
 

Recherche d'un mot dans l'arbre

La recherche se fait par une descente récursive dans l'arbre; à chaque descente, on regarde si le noeud en cours a un fils qui est identique à la première lettre du mot. Si c'est le cas, alors on "mange" le début du mot (la première lettre) et on cherche à partir de la position courante le mot restant. Si, à un moment, pendant l'exploration de l'arbre, on se retrouve avec un mot vide, alors le mot appartient à l'arbre. Attention : cette condition n'est valable que pour les arbres dont tous les mots ont la même longueur. Sinon, il faut rajouter une condition supplémentaire, et cette tâche vous revient.

function arbre.trouve(LeMot: string): boolean;
var lettre: char;
begin
 if LeMot = '' then
 trouve := true
 else
 begin
 lettre := LeMot[1];
 delete(LeMot, 1, 1);
 if courant.fils[lettre] = nil then
 trouve := false
 else
 begin
 courant := courant.fils[lettre];
 trouve := trouve(LeMot);
 end;
 end;
end;

Télécharger le code source Delphi