Le code Morse

En utilisant les techniques des arbres binaires, on peut facilement réaliser un programme qui représente graphiquement le code Morse par un arbre binaire. Dans cet arbre on considère seulement les lettres de A à Z, car leur représentation tient sur 5 niveaux. On rappelle que le code Morse est constitué de points et de tirets : ainsi le "S" est représente par 3 points "..." et le "O" par trois tirets "---". On considère que les points sont représentés par un fils gauche d'un noeud, et un tiret par un fils droit d'un noeud. Voici la représentation graphique d'un arbre contenant l'alphabet:

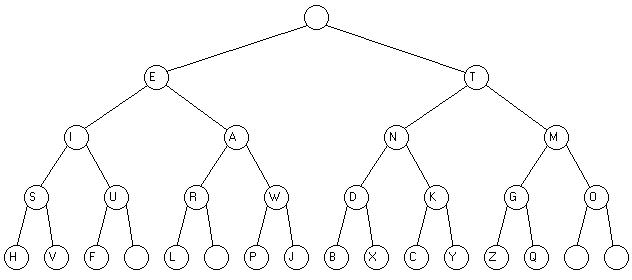Nous devons réaliser le programme qui dessine cet arbre. On utilise une chaîne de caractères pour stocker les lettres. Il faut savoir que l'alphabet Morse a plus de caractères que ce que nous avons choisi, qui font qu'un arbre binaire descend à sept niveaux. C'est pourquoi nous nous sommes limités seulement à 5 niveaux, et nous avons rempli les caractères manquants par des espaces.

Pour réaliser cet arbre, nous utilisons le parcours préfixe que nous avons vu précédemment et nous utilisons une formule mathématique afin d'introduire à chaque noeud de l'arbre le caractère correspondant.

La chaîne de caractères est donc, en fonction du parcours préfixe, la suivante :

const st : string = ' EISHVUF ARL WPJTNDBXKCYMGZQO ';

Les structures de données utilisées sont les suivantes :

noeud = class
private
 carac: char;
 gauche, droite: noeud;
 constructor create(c: char);
 destructor destroy;
 procedure creer(nb, niv: integer);
 procedure afficher(x, y, l: integer);
end;
 
arbre = class
private
 tete, courant: noeud;
public
 constructor create(c: char);
 destructor destroy;
 procedure afficher(x, y, l: integer);
end;
 
 
constructor noeud.create(c: char);
begin
 carac := c;
 gauche := nil; droite := nil;
end;
 
destructor noeud.destroy;
begin
 if gauche <> nil then gauche.destroy;
 if droite <> nil then droite.destroy;
end;
 
procedure noeud.afficher(x, y, l: integer);
begin
 with form1.image1.picture.bitmap.canvas do
 begin
 ellipse(x, y, x + 25, y + 25);
 textOut(x + 5, y + 5, carac);
 if gauche <> nil then
 begin
 moveto(x + 3, y + 20); lineto(x - (l div 2) + 10, y + 70);
 gauche.afficher(x - (l div 2), y + 60, l div 2);
 end;
 if droite <> nil then
 begin
 moveto(x + 22, y + 20); lineto(x + (l div 2) + 10, y + 70);
 droite.afficher(x + (l div 2), y + 60, l div 2);
 end;
 end;
end;
 
procedure noeud.creer(nb, niv: integer);
var i: integer;
begin
 if niv < 5 then
 begin
 gauche := noeud.create(st[nb + 1]);
 gauche.creer(nb + 1, niv + 1);
 i := nb + (round(exp((5 - niv) * ln(2))));
 droite := noeud.create(st[i]);
 droite.creer(i, niv + 1);
 end;
end;
 
//--------------------------------------
 
constructor arbre.create(c: char);
begin
 tete := noeud.create(c);
 courant := tete;
end;
 
destructor arbre.destroy;
begin
 courant := nil;
 tete.destroy;
end;
 
procedure arbre.afficher(x, y, l: integer);
begin
 tete.afficher(x, y, l);
end;
 
//--------------------------------------
 
 
procedure TForm1.FormCreate(Sender: TObject);
begin
 morse := nil;
 image1.picture.bitmap := tbitmap.create;
 with image1.picture.bitmap do
 begin
 width := 639; height := 500;
 end;
end;
 
procedure TForm1.Button1Click(Sender: TObject);
begin
 morse := arbre.create(' ');
 morse.tete.creer(1, 1);
end;
 
procedure TForm1.Button2Click(Sender: TObject);
begin
 morse.afficher(image1.width div 2 - 10, 10, image1.width div 2);
end;

Nous allons expliquer maintenant la création de l'arbre.

Le sommet contient un espace.

A gauche du sommet on a la lettre "E" et à droite la lettre "T", c'est à dire les positions 2 et 17 de notre chaîne de caractères "st". 2=1+1 et 17=1+16.

Au niveau suivant, à gauche du "E" on a "I" et à droite "A", c'est à dire les positions 3 et 10 de notre chaîne de caractères "st". Mais 3=2+1 et 10=2+8, où 2 est la position de "E" dans "st".

Au niveau suivant, à gauche de "I" on a "S" et à droite "U", c'est à dire les positions 4 et 7 de notre chaîne de caractères "st". Mais 4=3+1 et 7=3+4.

On constate donc que le fils gauche d'un noeud à la valeur du père incrémenté de 1 (on parle des caractères qui sont dans la chaîne "st" : "E"+1="I"; "I"+1="S") et que le fils droit à la valeur du père incrémenté de 2^5-niveau. On lit cela "2 élevé à la puissance (5-niveau)". On rappelle qu'ici le sommet de l'arbre est au niveau 1, donc la lettre "E" est au niveau 2; par conséquent, le fils droit de "E" sera incrémenté de 8, car 2³=8. De même, le fils droit du sommet sera incrémenté de 16, car 2^5-1 = 2⁴ = 16.

Télécharger le code source Delphi