Dérécursification des "tours de Hanoï"

Nous allons réaliser un programme itératif pour "dérécursifier" le problème des tours de Hanoï. La difficulté vient du fait que le programme des tours de Hanoï contient un double appel récursif avec des paramètres différents : après avoir effectué le premier appel récursif, tout change (le nombre de disques, les piquets).

Nous avons vu dans les chapitres précédents que, pour aboutir à une procédure récursive, on exécutait à la main un ensemble d'instructions, on regardait quelles étaient celles qui se répétaient, quelles étaient les variables utilisées, et on regroupait finalement les blocs identiques pour aboutir à une procédure récursive. Pour dérécursifier les tours de Hanoï, on va faire la même chose : on va réaliser à la main les mouvements des disques sur les 3 piquets, et on va essayer de trouver des similitudes ou des répétitions, afin d'en tirer un algorithme itératif.

Rappelons d'abord la définition récursive de la procédure :

H (n,depart,arrivee)

H (n-1,depart,intermédiaire)

Deplacer(depart,arrivee)

H (n-1,intermédiaire,arrivée)

Préliminaire

Nous allons noter Hn le déplacement de n disques (Hn est en fait le programme récursif, qui se résume à l'appel de la procédure). On symbolise "départ" par "d", "arrivée" par "a" et "intermédiaire" par "i".

La définition s'écrit alors :

Hn (d,a)

Hn-1 (d,i)

Deplacer(d,a)

Hn-1 (i,a)

Voici un dessin avec les trois piquets.

On décide que, si on a un nombre pair de disques à déplacer, on les déplace de 1 vers 3, et que, si on a un nombre impair de disques à déplacer, on les déplace de 1 vers 2. Cela est cohérent avec la définition récursive car, par exemple, pour déplacer cinq disques de 1 vers 3, en appliquant la définition, on déplace quatre disques (nombre pair) de 1 vers 2, puis un disque (nombre impair) de 1 vers 3 et enfin le reste de 2 vers 3.

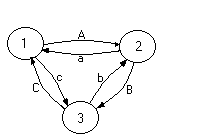
On note :

A le mouvement de 1 vers 2.

a le mouvement de 2 vers 1.

B le mouvement de 2 vers 3.

b le mouvement de 3 vers 2.

C le mouvement de 3 vers 1.

c le mouvement de 1 vers 3.

On décide de dire que :

les mouvements A et a sont de type 0.

les mouvements C et c sont de type 1.

les mouvements B et b sont de type 2.

Etudions quelques mouvements des disques :

H1 = A (de 1 vers 2)

H2 = A c B (1 vers 2; 1 vers 3; 2 vers 3)

H3 = A c B A C b A

H4 = A c B A C b A c B a C B A c B

On remarque que Hn, pour n supérieur à 2, est constitué d'une suite répétée de trois mouvements de types 0, 1 et 2. En effet, si l'on écrit Hn en majuscules, on obtient ACB ACB ACB..., avec éventuellement un A à la fin, la suite des mouvements ne pouvant se terminer que par A ou B (d'après ce que nous avons dit plus haut concernant la convention que nous avons adoptée suivant la parité de n).

Notons Gn la suite des mouvements de Hn, en faisant abstraction du sens du déplacement (ce qui revient à noter tous les mouvements en majuscules) :

Gn = A C B A C B A C B... (le dernier caractère étant un A pour n impair et un B pour n pair) pour n supérieur à 2, et G1=A. Gn n'est autre que Hn auquel il manque l'information de sens (distingué par les majuscules et les minuscules).

Ecrivons quelques valeurs de Gn :

G1 = A

G2 = A C B

G3 = A C B A C B A

G4 = A C B A C B A C B A C B A C B

Détermination du type du k-ième mouvement

On constate que:

1) pour n pair, Gn est une suite de ACB

2) pour n impair, Gn est une suite de ACB terminée par un A

Notons k l'indice d'un mouvement de Hn. Nous convenons que l'indice du premier mouvement est 0 (par exemple, pour H3, le mouvement d'indice 0 est A, le mouvement d'indice 1 est c, etc.).

Comme les mouvements se répètent tout les trois mouvements, pour connaître le type du k-ième mouvement de Hn, il suffit d'utiliser l'opérateur mathématique qui nous donne le reste de la division de k par 3, appelé opérateur modulo : le type du k-ième mouvement de Hn est donné par k mod 3, reste de la division entière de k par 3.

Exemple 1

Quel est le quatrième mouvement de H4 ?

Il s'agit du mouvement numéro 3, car les mouvements sont numérotés à partir de 0. Comme 3 mod 3 = 0, le quatrième mouvement de G4 est le même que le mouvement numéro 0, c'est à dire un A. Le quatrième mouvement de H4 est donc un mouvement de type 0. Nous ne savons pas encore en préciser le sens (A ou a).

Exemple 2

Quel est le sixième mouvement de H4 ?

Il s'agit du mouvement numéro 5, car les mouvements sont numérotés à partir de 0. Comme 5 mod 3 = 2, le sixième mouvement de G4 est le même que le mouvement numéro 2, c'est à dire un B. Le sixième mouvement de H4 est donc un mouvement de type 2. Nous ne savons pas encore en préciser le sens (B ou b).

Détermination du sens du déplacement : "A" ou "a" ?

On va placer les chaînes Hn et Gn l'une en dessous de l'autre pour les comparer facilement, puis créer une nouvelle chaîne de caractères, notée Sn constituée de 0 et de 1, qui présentera un 1 chaque fois qu'une majuscule de G remplace une minuscule de H, et un 0 sinon.

On définit ensuite la chaîne Un par :

- pour n pair : Un = Sn 0

- pour n impair Un = Sn 1

H1 = A (de 1 vers 2)

G1 = A

S1 = 0

U1 = 0 1

H2 = A c B (1 vers 2; 1 vers 3; 2 vers 3)

G2 = A C B

S2 = 0 1 0

U2 = 0 1 0 0

H3 = A c B A C b A

G3 = A C B A C B A

S3 = 0 1 0 0 0 1 0

U3 = 0 1 0 0 0 1 0 1

H4 = A c B A C b A c B a C B A c B

G4 = A C B A C B A C B A C B A C B

S4 = 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0

U4 = 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0

Comparons les différentes valeurs de Un.

Soit f la fonction définie par :

f(0)=01, f(1)=00 et f(ab)=f(a)f(b).

Appliquons cette fonction aux valeurs successives de Un.

f(U1) = f(01) = f(0) f(1) = 01 00 = U2

f(U2) = f(0100) = f(0) f(1) f(0) f(0) = 01 00 01 01 = U3

f(U3) = f(01000101) = f(0) f(1) f(0) f(0) f(0) f(1) f(0) f(1) = 01 00 01 01 01 00 01 00 = U4

On constate que Un = f(Un-1) = f(f(Un-2)) = f(f(f(Un-3))) = f(f(...f(U1)...)).

Il en résulte qu'un caractère sur deux de Un est toujours un 0. En effet, f(0) = 01 (ici le premier élément est 0, le deuxième étant 1) et f(1) = 00 (ici le premier élément est 0, le deuxième 0 aussi). Et comme Un est identique à Sn, à l'exception du dernier élément, on en déduit qu'un caractère sur 2 de Sn est égal à 0. Comme on compte le nombre de mouvements à partir de 0, alors les mouvements d'indices 0, 2, 4, 6, 8,... de Sn sont tous égaux à 0. Il en résulte que les mouvements correspondants dans Hn s'effectuent dans le sens indiqué par les majuscules.

Exemple 1

Quel est le cinquième mouvement de H4 ?

C'est le mouvement d'indice 4, car on compte à partir de 0. Comme 4 mod 3 = 1, le mouvement est de type 1 ("C" ou "c") puisque le mouvement numéro 1 de H4 est C. Comme dans U4 le mouvement numéro 4 est un 0 (le mouvement est d'indice pair), alors le cinquième mouvement de H4 est C, et non pas c.

Exemple 2

Quel est le treizième mouvement de H4 ?

C'est le mouvement d'indice 12, car on compte à partir de 0. Comme 12 mod 3 = 0, le mouvement est de type 0 ("A" ou "a") puisque le mouvement numéro 0 de H4 est A. Comme dans U4 le mouvement numéro 12 est un 0 (le mouvement est d'indice pair), alors le treizième mouvement de H4 est A, et non pas a.

Nous savons désormais trouver le sens d'un mouvement d'indice pair (en indexant à partir de zéro). Il nous reste à traiter le cas des mouvements d'indices impairs. Faisons d'abord une comparaison sur les Un successifs.

U1 = 0 1

U2 = 0 1 0 0

U2 = 0 1 0 0

U3 = 0 1 0 0 0 1 0 1

U3 = 0 1 0 0 0 1 0 1

U4 = 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 0

On a vu que U2 = f(U1). L'image du p-ième caractère de U1 (avec p=0 ou p=1) se trouve dans U2 à la position 2p et occupe les caractères d'indices 2p et 2p+1. On sait que U3 = f(U2). L'image du caractère d'indice p de U2 se trouve dans U3 aux positions 2p et 2p+1.

Exemple

L'image du caractère d'indice 0 par f de U2 se trouve dans U3 aux positions 0 et 1 (2*0=0 et 2*0+1=1). L'image du caractère d'indice 1 par f de U2 se trouve dans U3 aux positions 2 et 3 (2*1=2 et 2*1+1=3).

Ce phénomène est donc propagé par f au sein même des chaînes Un. Il est clair que les Un ont un nombre de caractères égal à une puissance de 2 (puisque f fait doubler le nombre de caractères à chaque application).

Exemple

Considérons le caractère d'indice 0 de U2 (c'est 0). Par f, nous obtenons 01 qui se trouve aux positions 0 et 1 (2*0=0 et 2*0+1=1). L'image par f du caractère d'indice 1 de U2 est 00, qui se trouve aux positions 2 et 3 (2*1=2 et 2*1+1=3).

Ainsi, dans la chaîne Un, le caractère qui se trouve à la position 2p est un zéro (comme on l'avait vu précédemment), et celui qui est à la position 2p+1 est un 0 ou un 1(cela dépend uniquement du caractère qui est à la position p) :

- si le caractère d'indice 2p+1 de Un est un 0, alors, à la position 2p on trouve la sous-chaîne 00, ce qui implique que son antécédent par f est un 1, donc à la position p on a un 1.

- si le caractère d'indice 2p+1 de Un est un 1, alors, à la position 2p on trouve la sous-chaîne 01, ce qui implique que son antécédent par f était un 0, donc à la position p on a un 0.

Notons Un[p] le caractère d'indice p de Un. D'après ce qui précède, on a :

Un[2p]=0

Un[2p+1] = 1 si Un[p] = 0

Un[2p+1] = 0 si Un[p] = 1

Ce qui se résume en deux lignes :

Un[2p] = 0

Un[2p+1] = 1 - Un[p]

Nous pouvons affiner ce dernier résultat : si p est un multiple de 2 (p=2k), alors les indices impairs (2p+1 et 2p+3) s'écrivent 4k+1 et 4k+3. Ainsi, Un[4k+1] = 1 - Un[2k] = 1-0 = 1 et Un[4k+3] = Un[2p+3] = Un[2(p+1)+1] = 1 - Un[p+1] = 1 - Un[2k+1] = 1 – (1- Un[k]) = Un[k].

Finalement :

Un[2k] = 0 : le mouvement d'indice 2k est codé par un 0 dans Sn, et donc le sens du mouvement correspondant dans Hn est un sens "majuscule".

Un[4k+1] = 1: le mouvement d'indice 4k+1 est codé par un 1 dans Sn, et donc le sens du mouvement correspondant dans Hn est un sens "minuscule".

Un[4k+3] = Un[k] : cette relation permet de calculer de proche en proche toutes les valeurs de Un[4k+3], puisqu'on connaît déjà Un[k] (k<4k+3).

Montrons par récurrence sur k que ces trois relations permettent bien de calculer de proche en proche tous les Un[k] :

Un[0] est connu (c'est 0).

Supposons que Un[k] soit connu pour tout entier inférieur ou égal à k.

k+1, comme tout entier naturel, est nécessairement de la forme 4q, ou 4q+1, ou 4q+2, ou 4q+3.

Si k+1=4q ou si k+1=4q+2, k+1 est pair et donc Un[k+1]=0, qui est donc connu.

Si k+1=4q+1, Un[k+1]=1, qui est donc connu.

Si k+1=4q+3, Un[k+1]=Un[q]. Comme k+1=4q+3, k=4q+2 et donc q<k. Un[q] est donc déjà connu en vertu de l'hypothèse de récurrence. CQFD.

Exemple

Nous savons maintenant calculer le sens d'un mouvement d'indice impair.

Quel est le quatorzième (celui d'indice 13) mouvement de H4 ?

Comme 13 mod 3 = 1, le quatorzième mouvement de G4 est le même que le mouvement numéro 1, c'est à dire un C. Le quatorzième mouvement de H4 est donc un mouvement de type 1 (C ou c). Quel est son sens ?

Prenons la chaîne U4 et déterminons son quatorzième caractère, correspondant à l'indice 13 (impair).

On a: 4*3+1=13, donc d'après les relations établies précédemment, U4[4*3+1] = 1. Ainsi, le mouvement numéro 13 de est codé par un 1 dans U4, donc également dans S4 : le sens du mouvement correspondant dans H4 est un sens "minuscule". Finalement, le quatorzième mouvement de H4 est c.

U4 = 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0

H4 = A c B A C b A c B a C B A c

Résumé

Pour déplacer n disques dans le problème des tours de Hanoï, il y a 2ⁿ-1 mouvements à effectuer (une unité de moins que la longueur de la chaîne Un).

Pour déterminer le type du mouvement d'indice k (le premier mouvement ayant l'indice 0), on calcule t = k mod 3.

Si t = 0, le mouvement est de type 0 (A ou a).

Si t = 1, le mouvement est de type 1 (C ou c).

Si t = 2, le mouvement est de type 2 (B ou b).

Pour déterminer le sens du mouvement :

Si k=4p (k = 0 mod 4), le sens est "majuscule".

Si k=4p+1 (k = 1 mod 4), le sens est "minuscule".

Si k=4p+2 (k = 2 mod 4), le sens est "majuscule".

Si k=4p+3 (k = 3 mod 4), le sens est le sens du mouvement d'indice p, nécessairement déjà connu.

Conclusion

On constate que la dérécursification des tours de Hanoï est basée sur la recherche d’un algorithme différent de celui récursif. Cela peut arriver souvent, surtout dans les algorithmes qui contiennent plusieurs appels récursifs, ce qui les rend difficilement transformables en algorithmes itératifs. Néanmoins, on sait aujourd’hui que tout algorithme récursif peut être dérécursifié.

Télécharger le code source Delphi (sans le dessin des piquets)

Télécharger le code source Delphi (avec le dessin des piquets)