La dérécursification des structures de données

Nous savons que la structure d'un arbre binaire est récursive. Nous allons voir comment on peut implémenter cette structure récursive dans une structure statique (c'est à dire un tableau de taille fixe). Voici d'abord la structure dynamique de l'arbre binaire (telle que nous l'avons vue dans le chapitre précédent) :

type Noeud =
 class
 private
 Fils: array['A'..'Z'] of Noeud; //liste de fils
 x, y: integer; // pour dessin arbre
 Gauche, Droite: Noeud;
 Lettre: char; // lettre contenue dans ce noeud de l'arbre
 Entier: boolean; //flag indiquant si le mot est entier
 public
 constructor create;
 destructor destroy;
 end; { Noeud }
 

Nous allons maintenant transformer cette structure dynamique en une structure statique, donc linéaire. Pour cela nous allons utiliser un tableau, dont chaque case a une structure représentée par :

- "lettre" : une variable de type "char"

- "fin" : une variable de type booléen, mais représentée ici par un byte, qui indique que le mot est entier

- "droite","bas" : représentent les deux fils gauche et droit de la structure dynamique.

type trec = record
 lettre: char;
 fin: byte;
 droite, bas: longint;
 end;
 
 dictionnaire = record
 t: array[1..5000] of trec;
 derniere_case: longint;
 end;
 
var dico: dictionnaire;
 

Nous avons utilisé un tableau de 5.000 cases; mais en plus le dictionnaire contient aussi une variable "derniere_case", de façon à ce qu'on sache où on doit implémenter dans le tableau tous les nouveaux mots.

Nous allons utiliser dans le programme à télécharger des mots de la même longueur, mais néanmoins, pour expliquer le principe de l'implémentation dans un tableau, nous utiliserons des mots de longueur différente. Voici une image illustrant parfaitement les types prédéfinis ci-dessus, ainsi que l'implémentation d'un petit arbre n-aire :

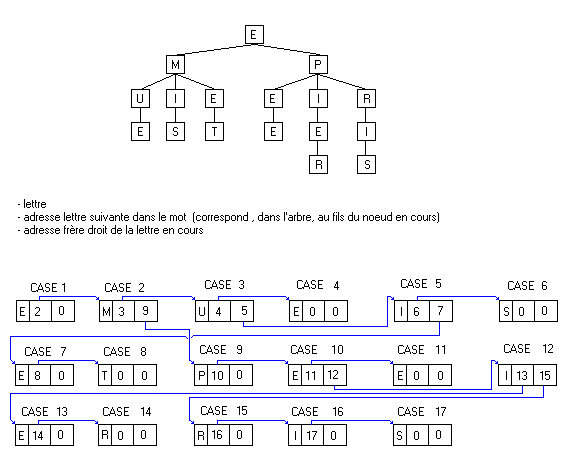Nous allons décrire brièvement une recherche de mot dans ce tableau. Supposons qu'on veuille trouver le mot "EPRIS". Nus sommes au début sur la case 1, donc sur la lettre E. On cherche ses fils. Le premier est à la case 2 et c'est M. Mais nous, on cherche la lettre P, donc on va se positionner sur le frère de M (M,3,9) qui est à la case 9. C'est bien un P, donc on descend maintenant sur son premier fils qui se trouve à la case 10 (car P,10,0). On trouve un E, qui ne nous intéresse pas, donc on va sur le frère de E qui se trouve à la case 12 (car E,11,12). C'est un I, il ne nous intéresse donc pas et on se positionne sur son frère qui se trouve à la case 15 (car I,13,15) et c'est bien un R. Le fils de R se trouve à la case 16 (car R,16,0) et c'est un I; le fils de I est à la case 17 et c'est un S. On a donc bien le mot EPRIS, car derrière le S il n'y a plus de fils, sinon le mot aurait été incomplet. On utilise aussi la variable "fin" pour indiquer que le mot est complet, auquel cas on peut ajouter d'autres lettres derrière ce mot (exemple : EPI et EPIER; les cases I et R ont la variable "fin" positionnée à 1, les autres à 0).

Voici la liste des procédures que nous allons utiliser :

1) - procédure introduis_mot_fin_dico(mot : string;p : longint;bas : boolean);

2) - function positionnement_sur_lettre(lettre : char;courant : longint; var dernier : longint ) : longint;

3) - procédure rajoute_mot(mot : string);

4) - function appartient(mot : string) : boolean;

La procédure 1) introduit un mot (ou la fin d'un mot) à la fin du dictionnaire. Elle a plusieurs paramètres :

- le mot à introduire dans le tableau

- la position à partir de laquelle on introduit le mot dans les cases du tableau

- une variable booléenne indiquant si le mot sera introduit en tant que fils de la case en cours (c'est donc la case "droite" qui est initialisée, cela correspondant à la lettre suivante dans le mot) ou bien en tant que frère (c'est donc la case "bas" qui sera initialisée);

exemple 1 : si on est sur la lettre I de EPIER et si on veut introduire la mot EPRIS, alors la lettre R sera introduite à droite de I en tant que fils de E. Si par la suite on cherche le mot EPRIS, on tombe premièrement sur le I, et comme il ne nous intéresse pas on prend le fils suivant de son père, donc R, suivi de I et de S.

exemple 2 : si on a introduit le mot EMIS, et si on est sur la lettre E et si on veut introduire le mot ROND, alors la lettre R sera mise en "bas" du E, en tant que frère de E.

Il faut savoir que dans tous les cas où l'on introduit un mot ou la fin d'un mot (pour le mot EPRIS on n'a introduit que RIS, car EP avait été introduit avec le mot EPEE), cette insertion se fera automatiquement à la fin du tableau (c'est à dire là où il y a des cases non remplies), donc à partir de la case numéro "derniere_case".

procedure introduis_mot_fin_dico(mot: string; p: longint; bas: boolean);
var l, courant: longint;
begin
 if bas
 then dico.t[p].bas := dico.derniere_case
 else dico.t[p].droite := dico.derniere_case;
 l := length(mot);
 for courant := 1 to l do
 with dico.t[dico.derniere_case + courant - 1] do
 begin
 lettre := mot[courant];
 fin := 0;
 droite := dico.derniere_case + courant;
 bas := 0;
 end;
 dico.t[dico.derniere_case + l - 1].droite := 0; // plus rien derrière
 dico.t[dico.derniere_case + l - 1].fin := 1; // c'est un mot
 inc(dico.derniere_case, l);
end;
 

La fonction 2) sert de positionnement sur une lettre, c'est à dire à trouver la case à partir de laquelle un mot sera introduit dans le tableau. Cette fonction a 3 paramètres :

- la lettre sur laquelle on veut se positionner

- la position à partir de laquelle on commence la recherche dans les cases

- la position de la dernière lettre trouvée (on a EPEE et on veut rajouter EPRIS; la dernière lettre trouvée est P et sa position dans le tableau sera retournée, car on va rajouter un R en tant que fils de P)

function positionnement_sur_lettre(lettre: char; courant: longint;
 var dernier: longint): longint;
var l: char;
begin
 l := dico.t[courant].lettre;
 if (courant > 0) and (l = lettre) then dernier := courant;
 while (courant <> 0) and (l <> lettre) do
 begin
  courant := dico.t[courant].bas;
 l := dico.t[courant].lettre;
 if (courant > 0)
 and (l = lettre)
 then dernier := courant; // mémorise la dernière position trouvée où l=lettre}
 end;
 positionnement_sur_lettre := courant;
end;
 

La procédure 3) représente le rajout d'un mot dans le tableau. Cette procédure utilise la procédure 1) et la fonction 2). Lors d'un rajout de mot dans notre tableau, nous devons réaliser dans l'ordre les opérations suivantes:

a) - nous positionner sur le noeud dont la lettre est identique à la première lettre du mot. Si le fils existe, alors on doit récupérer son numéro de case dans le tableau et recommencer avec la lettre suivante, sinon on doit récupérer le numéro de la case qui sera pointée par la case en cours.

exemple : dans le tableau décrit au dessin précédent, on a rempli les huit premières cases avec les mots EMUE,EMIS,EMET. La variable "derniere_case" est donc égale à 9. Si on veut rajouter EPEE, on doit récupérer le numéro 2, car P est le frère de M, et ainsi le numéro 9 se retrouve dans la case 2 : M,3,9. La case 9 est pointée par la case 2.

b) - arrivés ici, nous avons un choix à faire: ou bien nous avons trouvé au moins un début de mot qui était déjà dans le tableau (comme EP pour EPEE et EPRIS) et dans ce cas la variable "courant" est positive, ou bien on doit rajouter le mot en entier auquel cas la variable "courant" est nulle.

Si on a trouvé un début de mot, alors on est sur une case quelconque du tableau et on la fait pointer sur la case de numéro "derniere_case" où l'on rajoutera la suite du mot (exemple : on a dans le tableau le mot EPEE et on veut rajouter EPRIS. Le P pointe sur E et E n'a pas de frère, donc sa variable "bas" va pointer sur "derniere_case" où on va introduire le reste du mot, à savoir RIS).

Voici l'algorithme correspondant :

procedure rajoute_mot(mot: string);
var i, l, courant, p, precedent, dernier: longint;
 dedans: boolean;
begin
 l := length(mot); courant := 1; i := 1; dernier := 0;
 p := positionnement_sur_lettre(mot[1], 1, dernier);
 dedans := true;
 while (i <= l) and (p > 0) and
 (dedans) and
 (courant > 0) and
 (i < dico.derniere_case) do
 begin
 p := positionnement_sur_lettre(mot[i], courant, dernier);
 if p > 0 then courant := dico.t[p].droite;
 dedans := (dernier + 1) < dico.derniere_case;
  inc(i);
 end;
 if courant > 0 then //donc p=0
 begin
 dec(i);
 if dernier = 0 then // cas spécial
 begin
 if dico.derniere_case = 1
 then introduis_mot_fin_dico(mot, 1, false)
 else
 begin // positionnement sur la dernière lettre de la colonne d'un arbre
 p := courant;
 while p <> 0 do
 begin
 p := dico.t[p].bas;
 if p > 0 then courant := p;
 end;
 introduis_mot_fin_dico(mot, courant, true)
 end;
 end
 else
 if dernier + 1 = dico.derniere_case then
 if mot[i] = dico.t[dernier].lettre then
 introduis_mot_fin_dico(copy(mot, i, l), dernier, false)
 else
 introduis_mot_fin_dico(copy(mot, i, l), dernier, true)
 else
 begin // positionnement sur la dernière lettre de la colonne d'un arbre
 p := courant;
 while p <> 0 do
 begin
 p := dico.t[p].bas;
 if p > 0 then courant := p;
 end;
 introduis_mot_fin_dico(copy(mot, i, l), courant, true);
 end;
 end
 else // donc p<>0
 introduis_mot_fin_dico(copy(mot, i, l), dernier, false)
end;
 

Et maintenant il ne nous reste plus qu'à faire une fonction d'appartenance d'un mot. Elle est simple à réaliser; en effet, pour chacune des lettres du mot, à partir de la première et jusqu'à la dernière on appelle la fonction de positionnement sur une lettre donnée; si cette fonction échoue à un instant t, alors c'est que l'une des lettres du mot n'est pas dans les fils ou frères de la dernière lettre rencontrée; si, par contre, on arrive à la fin du mot, alors on doit tester que ce mot est bien terminé (la variable "fin" positionné à 1).

function appartient(mot: string): boolean;
var i, l, courant, p: longint;
 dernier: longint;
begin
 courant := 1; i := 1; p := 1; l := length(mot);
 while (i <= l) and (p > 0) do
 begin
 p := positionnement_sur_lettre(mot[i], courant, dernier);
 if p > 0 then courant := dico.t[p].droite;
 inc(i);
 end;
 appartient := (i > l) and (p > 0) and (dico.t[p].fin = 1);
end;

Télécharger le code source Delphi