Le jeu d'Othello

Un jeu assez répandu est le jeu d'Othello. Nous allons nous intéresser ici à la manière de programmer ce jeu. Nous allons décrire et expliquer par des exemples la manière classique de programmer le jeu d'Othello, et nous allons ensuite l'appliquer pour réaliser le programme. Pour faciliter l'explication nous commencerons par un exemple de fin de partie. L'avantage des fins de jeu est le suivant : la fonction d'évaluation d'un coup est très facile à réaliser, car elle consiste à faire le décompte des pions. Celui qui a le plus de pions après le dernier coup a gagné. Par contre, en début ou milieu de partie cette fonction est beaucoup plus difficile à réaliser, car il faut tenir compte du nombre de pions, de la valeur des cases (certaines cases ont une importance plus grande que d'autres, comme les coins), de la position des pions à un instant t... Il faudrait donc avoir l'avis d'un spécialiste de l'Othello.

Description des données et des procédures

Le plateau du jeu d'Othello sera un tableau à une dimension; ce tableau aura 100 cases et sera numéroté de 0 à 99. Ainsi, les cases du plateau seront 11, 12,...,18, 21,...,28,... jusqu'à 81,...,88. Le tableau de jeu s'appelle work, mais, pendant la réflexion, comme on va à plusieurs niveaux de profondeur, on est obligé de mémoriser plusieurs plateaux. Pour cela, on utilise le tableau tab_pense, qui peut contenir 19 niveaux de jeu (largement plus qu'il n'en faut; de plus, on peut changer quand on veut le nombre de plateaux qu'il contient).

On note les noirs par 0 et les blancs par 2. Les cases vides sont notées généralement avec un 8. Les cases vides qui sont autour d'un pion sont notées avec un 9. Ceci a été fait pour gagner du temps pendant le jeu. En effet, si on est en début de partie, on n'a que quatre pions. Comme la structure du tableau est linéaire, alors on avance linéairement dans le tableau jusqu'à ce qu'on trouve un 9. On sait alors qu'une case remplie avec un pion se trouve à proximité. Si on n'avait pas eu ce 9, alors, pour chacune des cases de l'échiquier on aurait été obligés de tester si on n'est pas en contact avec un pion.

Pour se déplacer dans les 8 directions, on utilise un tableau à 8 éléments appelé direction.

Pour essayer le programme, on a pris une situation de fin de partie un peu plus complexe que celle décrite dans les pages suivantes, afin de voir les performances du programme (coups, temps); le plateau représentant cette situation s'appelle work0. Sur cet othellier, on représente les pions du joueur par 2 et ceux de l'ordinateur par 0.On voit qu'il nous reste 11 coups à jouer. C'est pour cette raison qu'on a une variable profondeur, qui indique jusqu'à quel niveau l'ordinateur doit descendre pendant la réflexion.

Nous allons décrire maintenant les fonctions et les procédures afin de montrer à quoi servent les autres données.

Trouve_pos

Pour pouvoir jouer un coup, il faut d'abord trouver une case où placer son pion. La fonction qui trouve cette case s'appelle trouve_pos et elle a deux paramètres : niveau et joueur. Le paramètre niveau indique dans quel niveau (pendant la réflexion) il doit trouver un coup. Si, à ce niveau, on avait déjà joué un coup, il faut chercher un autre coup à partir de la position de ce pion déjà joué. On mémorise donc la dernière place trouvée dans un tableau, appelé dans le programme position. L'algorithme de la procédure est le suivant : on cherche un 9 dans l'othellier, puis on regarde les huit directions et si, dans une de ces directions, le pion joint au 9 est un pion ennemi et quelques cases plus loin on a un pion ami, alors c'est qu'on peut jouer à la place occupée par le 9.

Une fois qu'on a trouvé une position, il faut pouvoir placer le pion dans la case et retourner les pions dans toutes les directions possibles; la procédure qui fait cela s'appelle joue_coup.

Etant donné que nous sommes en fin de partie, la meilleure manière d'évaluer un coup est de compter combien de pions il rapporte. Pour cela, on a écrit la fonction compte_les_pions, qui compte les pions pour une couleur indiquée, blanc ou noir (joueur ou ordinateur). Le paramètre est ici inutile car l'ordinateur a les noirs. Il suffirait donc de comparer les pions directement à 0; mais ceci a été laissé au cas ou le lecteur voudrait modifier le programme.

Nous allons voir maintenant la principale procédure du programme, arbre. C'est la procédure qui s'applique à tous les jeux de réflexion, aussi nous allons l'expliquer avec des exemples.

Supposons qu'on va à 3 niveaux de profondeur. A chaque niveau, on joue les coups possibles un par un et, pour chaque coup, on explore l'arbre qui en découle. A chaque niveau final, on évalue la situation de l'échiquier et on retourne la note. Si le niveau 2 était un niveau du joueur, alors la note attribuée à ce niveau sera la plus petite note trouvée, car le but du joueur est que l'ordinateur obtienne la plus petite note possible. En revanche, au niveau 1, celui de l'ordinateur, l'ordinateur choisira le coup qui lui rapporte la plus grande note. Cette façon d'explorer un arbre et de retourner les notes, une fois les plus petites et une fois les plus grandes, s'appelle arbre min-max. Comme ici on explore un arbre en fin de partie, la fonction d'évaluation est faite par le compte des pions de l'ordinateur.

A chaque branche de l'arbre exploré on doit faire plusieurs étapes :

- faire les initialisations du niveau correspondant

- note attribuée au niveau

- le tableau "position" décrit ci-dessus

- le nombre de coups

Le nombre de coups sera utilisé au cas où aucun coup n'est possible au niveau actuel; dans ce cas, on doit "sauter" le niveau en cours et passer au niveau suivant en ayant pris soin d'incrémenter la profondeur; si, au niveau suivant, il n'y a pas de coup possible, alors c'est qu'on est arrivé à la fin de la partie et on évalue la situation.

repeter

- chercher un coup

- si trouvé, alors :

- jouer ce coup

- mémoriser le plateau de jeu

- descendre dans l'arbre si on n'est pas au niveau final, sinon

évaluer l'othellier

- si non trouvé, alors regarder si au niveau précédent on a pu jouer un

coup, auquel cas on continue à descendre dans l'arbre, sinon les

deux sont bloqués, donc niveau terminal, donc évaluation.

- faire l'élagage pour gagner du temps; l'élagage est expliqué par un arbre

dans les pages suivantes.

jusqu'à ce qu'il n'y ait plus de coups possibles.

La procédure arbre a deux paramètres, level (niveau, pour savoir à quel niveau de profondeur on est) et c (coefficient pour savoir qui doit jouer : soit le joueur, soit l'ordinateur; on appelle joue_coup avec le paramètre 1+c, qui vaut 0 ou 2; on n'a pas choisi des valeurs symétriques par rapport à 0 - comme dans le cas du le morpion -, car ici, on a un tableau de 100 bytes et non pas integer; or il faut gagner du temps pendant la réflexion, car il y a beaucoup de sauvegardes de plateaux).

Une fois le programme terminé, il ne nous restera plus qu'à écrire une fonction d'évaluation en cours de partie et de modifier la procédure arbre de façon à ce qu'elle n'appelle plus compte_les_pions, mais une autre fonction d'évaluation (malheureusement c'est ce qu'il y a de plus difficile à faire).

Nous allons étudier maintenant sur un exemple de fin de partie la programmation des jeux de réflexion. Nous allons voir la procédure alpha-beta (ou min-max) et aussi comment on doit faire un élagage (couper les branches d'un arbre), afin de gagner du temps pendant l'exploration d'un arbre (quelque soit le jeu de réflexion qu'on aura programmé). Nous allons illustrer ceci par un exemple concret (voir les images annexes).

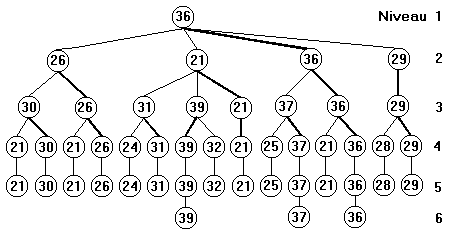La programmation de la réflexion d'un ordinateur se fait de la manière suivante : l'ordinateur simule un coup pour le joueur, ensuite un coup pour lui, ensuite pour le joueur et ainsi de suite jusqu'à ce qu'il atteigne la profondeur de jeu souhaitée. Une fois cette profondeur atteinte, il évalue le plateau et retourne la note trouvée. Pour les deux images qui illustrent notre étude (ou le dessin ci-dessus), la fonction d'évaluation est faite par le décompte des pions. On obtient successivement les notes 21, 30, 21, 26, 24, 31, 39, 32, 21, 25, 37, 21, 36, 28 et 29. Toutes ces notes seront retournées aux niveaux supérieurs. Mais que va-t-il se passer si un noeud a plusieurs fils ? Quelle note va-t-il choisir ? Pour chaque noeud de l'arbre, si le noeud se trouve à un niveau correspondant au coup du joueur (les blancs jouent) alors c'est la note la plus grande qui est retournée parmi les fils de ce noeud. C'est pourquoi, au niveau 3, on se retrouve avec les notes suivantes: 30, 26, 31, 39, 21, 37, 36, 29. Par contre, pour les niveaux correspondants aux coups de l'ordinateur, c'est la note la plus petite qui est retournée, ce qui explique qu'au niveau 2 on se retrouve avec les notes 26, 21, 36, 29. Mais au niveau 1, on prend la note la plus grande, d'où le 36 en haut de l'arbre, qui nous provient du troisième coup. L'ordinateur doit donc jouer le troisième coup. Cet algorithme s'appelle alpha-beta ou min-max, car, une fois sur deux, c'est la note maximale qui est retournée, et, une fois sur deux, la note minimale. Il est normal que parmi tous les coups qui s'offrent à lui, l'ordinateur cherche à minimiser la note de l'humain et à maximiser la sienne. On rappelle que c'est ce simple algorithme qui a battu Kasparov aux échecs (avec une puissance de calcul énorme, de l'ordre de 300 millions de coups à la seconde).

Mais, est-il bien utile d'explorer toutes les branches d'un arbre pendant le jeu ? N'y aurait-il pas un moyen de supprimer certaines branches de l'arbre, pour gagner du temps ? C'est ce que nous allons voir maintenant, avec l'opération d'élagage. Voici un dessin représentant un arbre, dont seulement le premier fils du noeud de niveau 2 a été visité en entier. On suppose que le noeud de niveau 2 a seulement 4 fils :

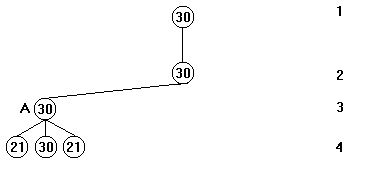
On explore d'abord le noeud A du niveau 3. On décide qu'à ce niveau l'ordinateur cherche à maximiser la note (il aurait très bien pu la minimiser). Le noeud A a trois fils, et le maximum est 30. Cette note est retournée au niveau précédent et comme c'est la première note à être retournée, alors elle devient la note témoin du niveau 2. On rappelle qu'au niveau 2, on cherche à minimiser les notes des fils. L'exploration du noeud A étant finie, l'ordinateur remonte au niveau 2, afin de parcourir les autres fils du niveau 2. Mais la note est retournée au niveau précédent (ceci est toujours valable : on retourne toujours la note au père du noeud en cours).

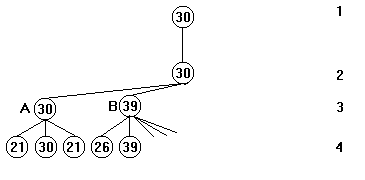Il passe ensuite au noeud B. Le premier fils de B rapporte 26. Le deuxième fils rapporte 39. Cette note est supérieure à 30 (témoin du niveau précédent). Alors l'exploration du noeud B s'arrête, étant devenue inutile. En effet, le noeud B a une note supérieure à la note témoin de son père. Et comme son père cherche à minimiser les coups, il choisira le noeud A. Donc à partir de maintenant, quelque soit la note trouvée parmi les fils de B, on sait que son père choisira le noeud A, d'où l'inutilité de l'exploration. Cette opération d'abandon de l'exploration des noeuds fils s'appelle élagage, et elle nous fait gagner beaucoup de temps pendant la réflexion de l'ordinateur. Continuons l'exploration de l'arbre.

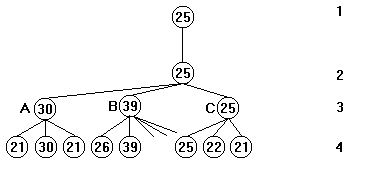
Au noeud C, l'exploration des fils continue tant qu'aucune note trouvée n'est supérieure à celle du père (qui jusqu'ici était de 30). Quand le noeud C a été complètement exploré, on constate que sa note est plus petite que celle de son père; elle est donc retournée et devient la nouvelle note témoin. On passe enfin au quatrième coup possible.

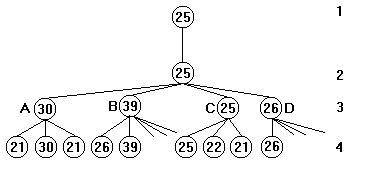
Le premier fils de D rapporte une note de 26. Comme cette note est supérieure à celle de son père, l'exploration de D est interrompue (élagage). En effet, l'ordinateur aurait pu trouver des notes supérieures à 26, mais de toutes façons, son père cherche à minimiser, et il aurait donc choisi le noeud C.

On peut donc résumer brièvement l'élagage :

1) on est sur un niveau qui maximise la note de ses fils.

- si la note de ce niveau est supérieure à celle de son père alors on arrête l'exploration et on retourne la note vers son père.

- tant qu'elle est inférieure, on continue l'exploration des fils.

- si on a terminé l'exploration, et si la note est inférieure à celle de son père, alors celle-ci est retournée et servira de témoin de comparaison avec les autres fils

2) on est sur un niveau qui minimise la note de ses fils

- si la note de ce niveau est inférieure à celle de son père alors on arrête l'exploration et on remonte la note vers son père.

- tant qu'elle est supérieure, on continue l'exploration des fils.

- si on a terminé l'exploration, et si la note est inférieure à celle de son père, alors celle-ci est retournée et servira de témoin de comparaison avec les autres fils

Voici le programme de fin de partie (on rappelle que l'ordinateur a les 0, représentés par la couleur noire, et que le joueur a les 2; il reste 11 cases à occuper donc la profondeur de l'arbre à explorer est de 11 ) :

const direction: array[1..8] of integer =
 (-11, -10, -9, -1, 1, 9, 10, 11);
 work0: array[0..99] of byte =
 (8, 9, 9, 9, 9, 9, 9, 9, 8, 8,
 8, 9, 0, 0, 0, 0, 0, 0, 9, 9,
 9, 9, 9, 0, 0, 0, 0, 9, 2, 9,
 9, 2, 2, 0, 0, 0, 2, 0, 2, 9,
 9, 2, 2, 0, 2, 2, 2, 0, 2, 9,
 9, 2, 2, 2, 2, 0, 0, 2, 2, 9,
 9, 2, 2, 2, 2, 0, 0, 2, 2, 9,
 9, 2, 9, 2, 0, 0, 0, 9, 9, 9,
 9, 9, 9, 2, 2, 2, 2, 2, 9, 9,
 9, 9, 9, 9, 9, 9, 9, 9, 9, 9);
 
 COEF_ORDINATEUR = -1;
 ORDINATEUR = 0;
 COEF_JOUEUR = 1;
 JOUEUR = 2;
 
type othellier = array[0..99] of byte;
 utile = array[0..18] of integer;
 n_othelliers = array[0..18] of othellier;
 
var work: othellier;
 position: utile;
 temoin: utile;
 nb_coups: utile;
 tab_pense: n_othelliers;
 profondeur: integer;
 
function compte_les_pions(couleur: integer): integer;
var x, total_pions: integer;
begin
 x := 10; total_pions := 0;
 repeat
 inc(x);
 if work[x] = couleur then inc(total_pions);
 until x = 88;
 compte_les_pions := total_pions;
end;
 
 
function trouve_pos(niveau, joueur: integer): integer;
var a, xx, xv, opposant, delta: integer;
begin
 xx := position[niveau];
 trouve_pos := 0;
 opposant := 2 - joueur;
 repeat
 repeat
 inc(xx)
 until (work[xx] = 9) or (xx > 88);
 position[niveau] := xx;
 if ((1 + xx) mod 10 > 1) and (xx < 89) then
 for a := 1 to 8 do
 begin
 delta := direction[a];
 if work[xx + delta] = opposant then
 begin
 xv := xx + delta;
 while work[xv] = opposant do
 inc(xv, delta);
 if work[xv] = joueur then
 begin
 trouve_pos := xx;
 exit
 end;
 end;
 end;
 until (xx > 88);
end;
 
 
procedure joue_coup(position_courante, joueur: integer);
var a, xx, opposant, delta: integer;
begin
 opposant := 2 - joueur;
 for a := 1 to 8 do
 begin
 delta := direction[a];
 xx := position_courante + delta;
 while work[xx] = opposant do
 inc(xx, delta);
 if work[xx] = joueur then
 repeat
 dec(xx, delta);
 work[xx] := joueur;
 until xx = position_courante;
 end;
 for a := 1 to 8 do
 if work[position_courante + direction[a]] = 8 then
 work[position_courante + direction[a]] := 9;
end;
 
 
procedure arbre(c, level: integer);
var x, next, last: integer;
begin
 nb_coups[level] := 0;
 position[level] := 10;
 temoin[level] := c * 25000;
 temoin[level + 1] := -temoin[level];
 next := level + 1;
 last := level - 1;
 repeat
 move(tab_pense[last], work, 100);
 x := trouve_pos(level, 1 + c);
 if x > 0 then
 begin
 inc(nb_coups[level]);
 joue_coup(x, 1 + c);
 move(work, tab_pense[level], 100);
 if profondeur <> level
 then arbre(-c, next)
 else temoin[next] := compte_les_pions(ORDINATEUR);
 end
 else
 if nb_coups[level] = 0 then
 if nb_coups[last] = 0
 then temoin[level] := compte_les_pions(ORDINATEUR)
 else begin
 move(work, tab_pense[level], 100);
 inc(profondeur);
 arbre(-c, next);
 dec(profondeur);
 end;
 case c of
 -1: begin
 if temoin[level] < temoin[next] then temoin[level] := temoin[next];
 if temoin[level] > temoin[last] then exit; //--- élagage
 end;
 1: begin
 if temoin[level] > temoin[next] then temoin[level] := temoin[next];
 if temoin[level] < temoin[last] then exit; //--- élagage
 end;
 end;
 until position[level] > 88;
end;
 
 
procedure niveau_un;
var x, meilleur_coup, temoin1: integer;
begin
 move(work, tab_pense[0], 100);
 meilleur_coup := 0;
 nb_coups[1] := 0;
 temoin[1] := 0;
 position[1] := 10;
 profondeur := 11;
 repeat
 move(tab_pense[0], work, 100);
 x := trouve_pos(1, ORDINATEUR);
 if x > 0 then
 begin
 inc(nb_coups[1]);
  if nb_coups[1] = 1 then meilleur_coup := x;
 joue_coup(x, 2);
 move(work, tab_pense[1], 100);
 arbre(COEF_JOUEUR, 2);
 temoin1 := temoin[1];
 if temoin[1] < temoin[2] then temoin[1] := temoin[2];
 if temoin[1] > temoin1 then meilleur_coup := position[1];
 end;
 until position[1] > 88;
 form1.memo1.lines.add('Le meilleur coup pour les noirs est ' + inttostr(meilleur_coup));
 form1.memo1.lines.add('Il rapporte ' + inttostr(temoin[1]) + ' pions noirs en fin de partie !');
end;
 
 
procedure tform1.affiche_jeu;
var x, y: integer;
begin
 for x := 1 to 8 do
 for y := 1 to 8 do
 if work[x + 10 * y] = JOUEUR then
 with image1.picture.bitmap.canvas do
 begin
 brush.color := clWhite;
 ellipse((x - 1) * 30 + 5, (y - 1) * 30 + 5, (x - 1) * 30 + 25, (y - 1) * 30 + 25);
 end
 else
 if work[x + 10 * y] = ORDINATEUR then
 with image1.picture.bitmap.canvas do
 begin
 brush.color := clBlack;
  ellipse((x - 1) * 30 + 5, (y - 1) * 30 + 5, (x - 1) * 30 + 25, (y - 1) * 30 + 25);
 end;
end;
 
procedure TForm1.FormShow(Sender: TObject);
var i: integer;
begin
 image1.picture.bitmap := tbitmap.create;
 with image1.picture.bitmap do
 begin
 width := 240;
 height := 240;
 canvas.brush.style := bsSolid;
 for i := 1 to 7 do
 with image1.picture.bitmap.canvas do
 begin
 moveto(i * 30, 0); lineto(i * 30, 240);
 moveto(0, i * 30); lineto(240, i * 30);
  end;
 end;
 image1.autosize := true;
 move(work0, work, 100); fillchar(temoin, sizeof(temoin), #0);
 affiche_jeu;
end;
 
procedure TForm1.Button1Click(Sender: TObject);
begin
 niveau_un;

end;

Télécharger le code source Delphi