Génération récursive de courbes fractales
Les courbes fractales sont des courbes possédant la propriété d'autosimilarité : chacune des parties de la courbe est semblable à n'importe quelle autre. Qu'on s'approche aussi près que l'on veut de la courbe, et on verra toujours la même chose ! Par exemple, le pourtour d'une côte, les arbres et les nuages ont des structures fractales qui peuvent être modélisées mathématiquement.
Nous allons prendre pour exemple la très célèbre courbe en flocon de neige de Von Koch (1904).
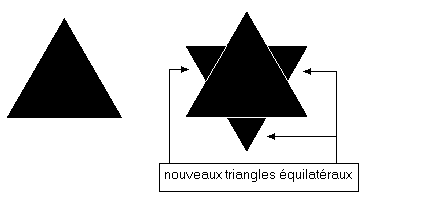
Cette courbe est obtenue en partant d'un triangle équilatéral. Sur chaque côté, on construit à l'extérieur du triangle, sur le tiers central, un nouveau triangle équilatéral. En poursuivant à l'infini, on obtient la courbe de Von Koch. Cette courbe n'est pas rectifiable (sa longueur est infinie), elle est continue (elle ne comporte aucun trou) et elle n'est différentiable presque nulle part (il est impossible de construire une tangente en presque chacun de ses points - en mathématiques, on dit qu'un ensemble E possède une propriété P presque partout si on a P pour tous les points de E sauf pour un sous-ensemble dénombrable de points de E -).
Algorithme du programme « Flocon de Von
Koch »
Variables globales :
Ecrx, Ecry : Largeur et hauteur de l'écran
Le tracé est réalisé par deux procédures, la principale étant la procédure Koch.
Définition de la procédure récursive
« segment »
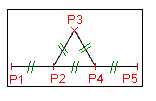
Ses paramètres sont x1,y1,x5,y5, c'est-à-dire les cordonnées des extrémités P1 et P5 du "segment" à tracer.
Variables locales :
l : longueur du segment P1P5
x2,x3,x4,y2,y3,y4 : abscisses et ordonnées des points P2, P3, P4.
Calculer la longueur de P1P5 et la stocker dans l
Si la longueur est inférieure à 2 pixels alors tracer le segment P1P5 (en informatique, rien n'est infini !)
Sinon :
Calculer les coordonnées des points P2 et P4, respectivement barycentres de {(P1,2)(P5,1)} et de {(P1,1)(P5,2)}.
On utilise la formule des barycentres pour couper un segment en trois. Un exemple concret de barycentres est le suivant : on a une poutre avec un poids de 2 kilos à un bout, et un poids de 1 kilo à l'autre bout. La formule du barycentre nous donne le point exact de la poutre où celle-ci est en équilibre.
Dans le programme, comme on l'a dit au début, on dessine sur chaque côté un nouveau triangle équilatéral; mais ce nouveau triangle sera incliné; les triangles qui seront construits sur ses côtés seront aussi inclinés, mais auront un autre angle d'inclinaison, donc nous sommes obligés d'utiliser les formules de rotation dans le plan.
Calculer les coordonnées du point P3, image de P4 par la rotation d'angle 60° et de centre P2
(on montre
que x3=x2/2-cos30*y2+x4/2+cos30*y4 et que y3=cos30*x2+y2/2-cos30*x4+y4/2)
Appeler la procédure segment avec les paramètres (x1,y1,x2,y2),
Appeler la procédure segment avec les paramètres (x2,y2,x3,y3),
Appeler la procédure segment avec les paramètres (x3,y3,x4,y4),
Appeler la procédure segment avec les paramètres (x4,y4,x5,y5).
Définition de la procédure Koch
Sans paramètres
Variables locales :
x0, y0 : coordonnées du point de départ du tracé taille : longueur des côtés du triangle initial
Sélectionner une couleur (blanc)
Définir la taille (on prend la moitié de la largeur de l'écran)
Définir x0 pour que le flocon soit centré horizontalement (largeur de l'écran/4)
Définir y0 pour que le flocon soit centré verticalement
Appeler la procédure segment avec les paramètres :
x0, y0, x0+taille, y0
x0+taille, y0, x0+taille/2, y0+cos30*taille
x0+taille/2, y0+cos30*taille, x0, y0
Génération itérative de courbes fractales
Nous allons donner un exemple bien connu de dessin fractal, celui de la courbe de Mandelbrot. Ce dessin est réalisé de façon itérative avec une boucle, à cause de la simplicité de la fonction utilisée; par contre, le dessin du flocon de Von Koch (1904) est récursif.
La courbe de Mandelbrot utilise les nombres complexes, donc le dessin s'effectue dans le plan complexe.
Le programme affiche un dessin qui est l'ensemble des points du plan complexe d'affixe z tels que la suite (|z(n)|) pour n entier naturel, soit convergente, avec : z(0)=z0 et z(n+1)=[z(n)]2+z0.
Vous pouvez initialiser le paramètre "seuil de divergence" à 10, et changer le progressivement de 10 en 10 par exemple. Cela vous permettra de suivre l'évolution de la courbe et des couleurs ("déplacement" progressif).
Vous pouvez aussi changer la variable "profondeur de calcul". Une initialisation à 10 suivi d'une augmentation progressive de 10 en 10 vous permettra de voir la courbe se dessiner à l'écran d'une façon de plus en plus précise.
procedure Dessine;
var large, haut, iimag, ireal, prof: integer; dreal, dimag, lreal, limag, re, im, xx, yy: real;
begin
large := Form1.Image1.Width; haut := Form1.Image1.Height; Form1.Image1.Canvas.Brush.Style := bsSolid; Form1.Image1.Canvas.Brush.Color := clWhite;Form1.Image1.Canvas.Rectangle(0, 0, large, haut);
dreal := (re_max - re_min) / large; dimag := (im_max - im_min) / haut;for iimag := 0 to haut - 1 do
for ireal := 0 to large - 1 do begin
lreal := re_min + ireal * dreal;
limag := im_min + iimag * dimag; re := lreal; im := limag;prof := 0;
repeat xx := re * re;yy := im * im;
im := 2 * re * im - limag;
re := xx - yy - lreal;
inc(prof); until (prof = calprof) or (xx + yy > infini); if prof < calprof then beginif prof > desprof then Form1.Image1.Canvas.Pixels[ireal, iimag] := color(prof mod 19)
else if ((prof mod 2) = 0) then Form1.Image1.Canvas.Pixels[ireal, iimag] := color(prof mod 19);
end;end; //next ireal
end;
procedure TForm1.Button1Click(Sender: TObject);
begin
infini := StrToFloat(Edit5.Text); // le nombre que l'on considère comme "infini" (seuil de divergence)
calprof := StrToInt(Edit6.Text); // profondeur de calcul (nombre d'itérations pour tester la convergence)
desprof := StrToInt(Edit7.Text); // profondeur de dessin (nb de couleurs utilisées)
re_min := StrToFloat(Edit1.Text); // x min
re_max := StrToFloat(Edit2.Text); // x max
Im_min := StrToFloat(Edit3.Text); // y min
Im_max := StrToFloat(Edit4.Text); // y max
if infini <= 0 then infini := 10;
if calprof <= 0 then calprof := 20;
if desprof <= 0 then desprof := 10;
if re_min > re_max thenbegin
x := re_min;re_min := re_max;
re_max := x;end;
if Im_min > Im_max then beginx := Im_min;
Im_min := Im_max; Im_max := x;end;
Screen.Cursor := crHourGlass; Dessine; Screen.Cursor := crDefault;end;
Télécharger le code source Delphi (Von Koch)
Télécharger le code source Delphi (Mandelbrot)