Les petits chiens

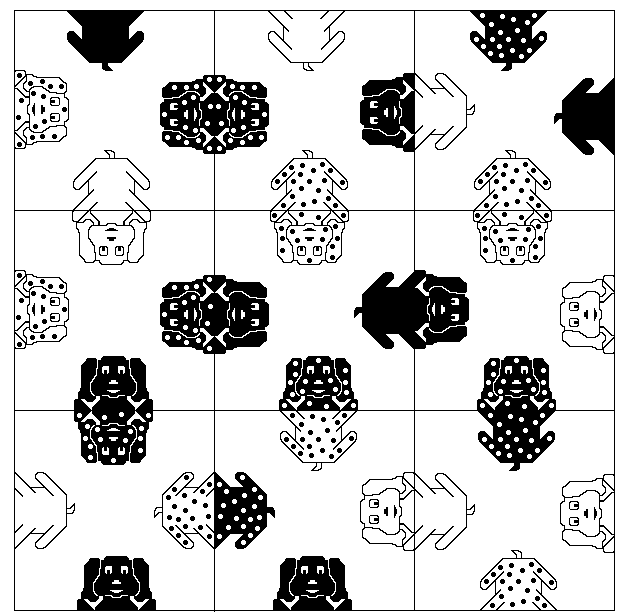
Un problème amusant et pouvant être facilement résolu par l'ordinateur est le problème des petits chiens: on dispose de neuf cartes, chacune contenant quatre têtes ou corps des chiens; le but du jeu est de placer les cartes de manière à avoir réunis la tête et le corps des chiens de même couleur; il y a plusieurs possibilités et comme pour le problème des 8 reines ou du cavalier, nous allons utiliser la récursivité. Les cartes doivent former un carré.

Il est évident qu'il faut former des combinaisons des 9 cartes; pour cela on utilise le programme des anagrammes; on se sert de la deuxième solution, car elle est plus rapide.

procedure combinaisons;
var ch: string;
 l: byte;
 
 procedure EchangeCar(var ch: string; i, j: byte);
 var car: char;
 begin
 if i <> j then
 begin
 car := ch[i];
 ch[i] := ch[j];
 ch[j] := car;
 end
 end;
 
 procedure anagram(ch: string; i: byte);
 var j: byte;
 begin
 if i = l then memo1.lines.add(ch)
 else
 for j := i to l do
 begin
 EchangeCar(ch, i, j);
 Anagram(ch, i + 1);
 EchangeCar(ch, i, j);
 end;
 end;
 
begin
 ch := 'abc'; l := length(ch);
 anagram(ch, 1);
end;

Cette procédure est insuffisante pour résoudre le problème, car les cartes peuvent tourner sur elles-mêmes, quatre fois chacune. Donc pour chaque combinaison obtenue de 9 cartes, il faut faire tourner les cartes et vérifier que la position obtenue crée 12 chiens, sinon il faut essayer une autre position.

Pour vérifier que les chiens sont en position, on fait les tests suivants:

- on pose la première carte

- on pose la deuxième; l'ouest de la deuxième doit correspondre à l'est de la première

- on pose la troisième; l'ouest de la troisième doit correspondre à l'est de la deuxième

- on pose la quatrième; le nord de la quatrième doit correspondre au sud de la première

- on pose la cinquième; le nord de la cinquième doit correspondre au sud de la deuxième et l'ouest de la cinquième doit correspondre à l'est de la quatrième

- on pose la sixième; le nord de la sixième doit correspondre au sud de la troisième et l'ouest de la sixième doit correspondre à l'est de la cinquième

- on pose la septième; le nord de la septième doit correspondre au sud de la quatrième

- on pose la huitième; le nord de la huitième doit correspondre au sud de la cinquième et l'ouest de la huitième doit correspondre à l'est de la septième

- on pose la neuvième; le nord de la neuvième doit correspondre au sud de la sixième et l'ouest de la neuvième doit correspondre à l'est de la huitième

On fait donc une fonction qui vérifie ce qu'il faut en fonction du numéro de la carte passée en paramètre; mais pour vérifier qu'une tête correspond à un corps, on numérote les têtes avec des valeurs positives et les corps correspondants avec des valeurs négatives, de sorte que la somme de la tête et du corps du même chien fasse zéro. En faisant les sommes on peut donc vérifier si une carte est bien placée.

Ensuite pour chaque combinaison obtenue avec les anagrammes, on fait les rotations; la procédure qui s'occupe des rotations fait les étapes suivantes :

- elle a un paramètre qui est le numéro de la carte à tourner

- elle fait une boucle 4 fois pour tourner la carte

- si la carte est bien placée (vérification avec la fonction ci-dessus) alors elle s'appelle elle-même avec un paramètre correspondant au numéro de la carte suivante;

- si le paramètre est 10, alors c'est qu'elle a déjà tourné 9 cartes et qu'elles sont toutes bien placées; c'est donc la solution, et on affiche les 9 cartes.

Le nombre de possibilités (façon d'arranger les cartes) est de (4⁹)*9! possibilités. C'est à dire environ 95 milliards, ce qui en fait un bon paquet pour un jeu aussi simple à première vue!

Voici le programme correspondant :

type carte = record
 nord, est, sud, ouest: integer;
 end;
 
const TETE1 = 1; CORPS1 = -1; {--- rouge ---}
 TETE2 = 2; CORPS2 = -2; {--- vert ---}
 TETE3 = 3; CORPS3 = -3; {--- bleu ---}
 TETE4 = 4; CORPS4 = -4; {--- jaune ---}
 
var t: array[1..9] of carte;
 longueur: byte;
 st: string;
 ch: char;
 car: carte;
 nb: longint;
 num: integer;
 
 
//************************************************************************
 
function carte_ok(nb: integer): boolean;
begin
 case nb of
 1: carte_ok := true;
 2: carte_ok := t[1].est + t[2].ouest = 0;
 3: carte_ok := t[2].est + t[3].ouest = 0;
  4: carte_ok := t[1].sud + t[4].nord = 0;
 5: carte_ok := (t[2].sud + t[5].nord = 0) and (t[4].est + t[5].ouest = 0);
 6: carte_ok := (t[3].sud + t[6].nord = 0) and (t[5].est + t[6].ouest = 0);
 7: carte_ok := (t[4].sud + t[7].nord = 0);
 8: carte_ok := (t[5].sud + t[8].nord = 0) and (t[7].est + t[8].ouest = 0);
 9: carte_ok := (t[6].sud + t[9].nord = 0) and (t[8].est + t[9].ouest = 0);
 end;
end;
 
procedure init_carte(var c: carte; nord, est, sud, ouest: integer);
begin
 c.nord := nord; c.est := est; c.sud := sud; c.ouest := ouest;
end;
 
procedure initialisation;
begin
 num := 0;
 st := '123456789';
 init_carte(t[1], CORPS1, TETE4, CORPS2, TETE3);
 init_carte(t[2], TETE2, TETE4, TETE1, TETE3);
 init_carte(t[3], CORPS3, TETE4, CORPS2, TETE1);
 init_carte(t[4], CORPS1, TETE4, TETE1, TETE3);
 init_carte(t[5], CORPS3, TETE2, TETE1, CORPS4);
 init_carte(t[6], TETE2, TETE4, TETE1, TETE3);
 init_carte(t[7], CORPS1, CORPS3, CORPS2, CORPS4);
 init_carte(t[8], TETE4, CORPS3, TETE1, CORPS2);
 init_carte(t[9], TETE2, CORPS3, CORPS2, CORPS4);
end;
 
procedure rotation_droite(var c: carte);
var b: integer;
begin
 b := c.nord;
 c.nord := c.ouest; c.ouest := c.sud; c.sud := c.est; c.est := b;
end;
 
procedure rotations(numero: integer);
var i: integer;
begin
 if numero = 10 then
 begin
 Dessine(Form1.Image1.Canvas, 0, 0, Form1.Image1.Width div 3);
 Screen.Cursor := crDefault;
 inc(num);
 Form1.Label1.Caption := 'Solution ' + IntToStr(num);
 showmessage('Solution ' + IntToStr(num) + ' - Cartes : ' + st);
 Screen.Cursor := crHourGlass;
 end
 else
 for i := 1 to 4 do
 begin
 rotation_droite(t[numero]);
 if carte_ok(numero) then rotations(numero + 1);
 end;
end;
 
procedure anagram(i: byte);
var j: byte;
begin
 if i = 9 then rotations(1)
 else
 for j := i to 9 do
 begin
 car := t[i]; t[i] := t[j]; t[j] := car;
 ch := st[i]; st[i] := st[j]; st[j] := ch;
 anagram(i + 1);
 car := t[i]; t[i] := t[j]; t[j] := car;
 ch := st[i]; st[i] := st[j]; st[j] := ch;
 end
end;

Télécharger le code source Delphi