La maison

Soit la figure suivante :

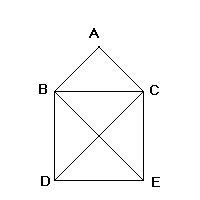
On demande de faire le programme qui trace cette maison en un seul coup, c'est à dire sans "lever le crayon".

Structure des données

Nous devons d'abord représenter la maison en mémoire; on voit que la maison a 5 sommets : A, B, C, D, E. Pour représenter cela, nous allons utiliser un tableau de 2 dimensions qui contiendra 5 lignes et 5 colonnes.

Ensuite, dans ce tableau, on va représenter tous les chemins qu'on peut tracer par un 0 et tous les chemins qu'on ne peut pas tracer (ou qui ont déjà été tracés) par un 1.

On ne peut pas aller de A à A, donc dans le tableau, aux coordonnées (0,0) nous avons un 1; de même pour les autres sommets. Donc la diagonale du tableau (représentant les chemins AA,BB,CC,DD,EE) est mise à 1; en regardant la maison on voit qu'on ne peut pas aller de A à D (donc de D à A non plus) et de A à E (donc de E à A non plus); pour indiquer qu'on ne peut pas (ou plus) aller de A à D, on remplit le tableau en première ligne et quatrième colonne avec 1; pour indiquer qu'on ne peut pas aller de D à A on remplit le tableau en quatrième ligne (car D est le quatrième élément) et première colonne (car A est le premier élément) avec un 1. Idem pour AE.

Analyse de l'algorithme

Faisons une petite analyse du programme:

- on compte les segments à dessiner: il y en a 8 : AB,AC,BC,BD,BE,CD,CE,DE.

- nous allons faire tous les essais possibles sur cette maison; on va donc commencer à la première ligne du tableau et parcourir les colonnes jusqu'à trouver un 0, ce qui indique qu'on peut aller vers ce sommet (par exemple nous sommes à la première ligne, donc au sommet A, et on parcourt les colonnes de cette ligne; on trouve un 0 à la deuxième colonne, donc on peut aller à B; on occupe immédiatement cette case ainsi que celle qui va de B vers A, et on démarre maintenant à la ligne correspondant à B, c'est à dire à la deuxième ligne; la première colonne vide est celle qui correspond à C, étant donné que BA a été rempli ci-dessus; on remplit les cases correspondant aux chemins BC et CB et on démarre à la ligne correspondant à C, c'est à dire la troisième ligne, et ainsi de suite.

- tout ceci se fait par des appels récursifs; la procédure récursive s'appelle "cherche" et elle a 3 paramètres :

- y: c'est le sommet d'où on part, c'est à dire la ligne en cours dans le tableau

- niveau: c'est la variable qui indique combien de segments on a tracé; si on a tracé le huitième segment, alors un appel récursif a lieu avec niveau=9; ceci est le point d'arrêt et on affiche les positions accumulées dans le paramètre "st"

- st : chaîne de caractères qui mémorise le chemin parcouru

Le programme

Voici le programme correspondant :

procedure TForm1.Button1Click(Sender: TObject);
type tab = array[0..4, 0..4] of integer;
 
const t1: tab =
 ((1, 0, 0, 1, 1),
 (0, 1, 0, 0, 0),
 (0, 0, 1, 0, 0),
 (1, 0, 0, 1, 0),
 (1, 0, 0, 0, 1));
 
var t: tab;
 
 procedure cherche(colonne, niveau: integer; st: string);
 var ligne: integer;
 begin
 if niveau = 9 then
 memo1.lines.add(st)
 else
 for ligne := 0 to 4 do
 if t[ligne, colonne] = 0 then
 begin
 st := st + chr(65 + colonne) + chr(65 + ligne) + ' ';
 t[ligne, colonne] := 1; t[colonne, ligne] := 1;
 cherche(ligne, niveau + 1, st);
 t[ligne, colonne] := 0; t[colonne, ligne] := 0;
 delete(st, length(st) - 2, 3);
 end;
 end;
 
 procedure recherche;
 var colonne: integer;
 begin
 memo1.lines.clear;
 move(t1, t, sizeof(t));
 for colonne := 0 to 4 do
 cherche(colonne, 1, '');
 end;
 
begin
 recherche;
end;

Télécharger le code source Delphi