Ecrire un nombre en toutes lettres
Introduction
De nos jours, de nombreux programmes doivent convertir des sommes en lettres. Nous vous présentons ici un programme qui traduit un nombre entier (une suite de chiffres) quelconque en son expression littérale correspondante en français (exemple : 314 = « trois cent quatorze »). Le programme traite les nombres décimaux en traitant de façon distincte la partie entière et celle décimale, puis concatène ensuite les deux. Il peut être utilisé par exemple dans les logiciels qui impriment des chèques.
Nous allons découvrir quels sont les problèmes liés à la langue française qui peuvent apparaître dans ce programme.
Façon d’écrire un nombre en toutes
lettres en français
Problèmes d’écriture
Nous allons étudier un peu les différents cas qui peuvent se présenter.
Unités :
Le chiffre des unités ne pose aucun problème, chaque chiffre a un correspondant littéral :
0= « zéro » , 1 = « un », 2= « deux » et ainsi de suite.
Dizaines :
Par contre, dès qu’on arrive aux dizaines, les choses se
compliquent car la façon d’écrire et de prononcer les nombres
varie selon le chiffre utilisé. Ainsi on dit « onze » au lieu de
« dix et un » (par contre on dit « vingt et un ») , on dit « douze » au lieu de « dix-deux » (par contre on dit
« vingt-deux ») et ainsi de suite jusqu’à seize. Mais à partir de là on dit bien « dix-sept » (de
même que « vingt-sept »), « dix-huit », etc.
Le cas
du mot « et » (conjonction
de coordination)
Noter le fait qu’on
rajoute le mot « et » pour le chiffre « 1 » (vingt ET un,
trente ET un, quarante ET un, cinquante ET un, soixante ET un, soixante ET
onze) mais pas pour les autres dizaines.
D’autres particularités concernent le soixante-dix, quatre-vingt, quatre-vingt-dix. Ces cas sont spécifiques au français utilisé en France, qui est différent de celui utilisé en Suisse, où il y a une façon bien plus simple de dire ces nombres : septante, huitante, nonante (et c’est très logique ! ) , ou en Belgique qui utilise « septante, octante, nonante »
On constate qu’on a trois cas où on utilise « onze » (11,71,91) et 7 cas où on utilise « un » (1,21,31,41,51,61,81).
En plus de cela, il y a les cas des mots « vingt » et « quatre-vingt »:
VINGT
1. L'adjectif numéral prend la marque du pluriel s'il est multiplié par un
nombre et s'il n'est pas suivi d'un autre adjectif de nombre.
Exemple : Quatre-vingts feuilles, quatre-vingt-huit francs.
Attention aux mots million, milliard qui ne sont pas des adjectifs numéraux, mais des noms.
Exemple : Quatre-vingts millions.
Précédé de cent ou de mille, l'adjectif numéral est toujours invariable.
Exemple : Cent vingt personnes.
2. Dans les adjectifs numéraux composés, le trait d'union s'emploie seulement
entre les éléments qui sont l'un et l'autre inférieurs à cent, sauf si ces
éléments sont joints par la conjonction « et ».
Exemple : Vingt et un.
Vingt-cinq.
QUATRE-VINGT(s) adj. et n. m. ·
Adjectif numéral cardinal. Quatre fois vingt.
Il a quatre-vingts ans, elle a quatre-vingt-deux ans.
Note.- L'adjectif numéral cardinal s'écrit avec un « s » s'il est
multiplié par un nombre et s'il n'est pas suivi d'un autre adjectif numéral.
· Adjectif numéral ordinal invariable.
Exemple : Quatre-vingtième.
La page quatre-vingt. En mil neuf cent quatre-vingt.
· Nom masculin invariable.
Exemple : Des quatre-vingt en lettres lumineuses.
Notes.-
1. Attention aux nombres composés des mots million, milliard qui ne sont pas
des adjectifs numéraux, mais des noms et qui permettent donc la marque du
pluriel à vingt si l'adjectif numéral est multiplié par un nombre.
Exemple : Quatre-vingts
millions de francs.
2. Après l'adjectif numéral, la conjonction « et » ne s'emploie pas
devant « un » , contrairement à
« trente et un », « quarante et un »...
Exemple : Quatre-vingt-un
citrons, quatre-vingt-une tomates.
3. Les adjectifs numéraux composés de quatre-vingt s'écrivent avec des traits
d'union.
Exemples : Quatre-vingt-deux, quatre-vingt-trois, quatre-vingt-dix, quatre-vingt-onze,
quatre-vingt-dix-sept.
Centaines :
Pour les centaines c’est plus simple, car le seul cas particulier qui existe est celui de « cent » (on ne dit pas « un cent » mais « cent » tout court), tous les autres multiples de 100 ayant le nom du chiffre devant : « deux cent » , « trois cent »…
Le problème du « s » (utilisé dans certains cas pour le pluriel de « cent ») est traité ici.
L'adjectif
« cent » :
-
il prend un
« s » quand il est multiplié par un autre nombre et qu'il termine
l'adjectif numéral.
exemple : J'ai
lu sept cents pages.
-
il est invariable
quand il n'est pas multiplié par un autre nombre
Exemple :
Il a lu cent pages.
-
il est invariable
quand il est suivi d'un autre nombre.
Exemple : Elle a écrit trois
cent vingt-sept pages.
-
devant millier,
million, milliard , il s'accorde quand il n'est pas
suivi d'un nom de nombre.
Exemple :
Quatre cents millions de francs.
Le reste
Au delà de mille, million, milliard les nombres s’écrivent de la même façon, et ils sont lus par groupes de 3 chiffres.
On voit donc qu’il est important
de connaître le nombre de chiffres des nombres pour bien les prononcer.
Paradoxalement, il est clair que si la lecture d’un nombre se fait bien (tout
comme un mot) de gauche à droite, sa prononciation dépend fortement des
groupements de trois chiffres que l’on peut opérer à partir de la droite cette
fois. D’où l’intérêt d’un caractère séparateur de milliers (caractères
« espace » ou « . ») pour faciliter cette lecture dans la vie courante (exemple : 1.325.240), comme on le voit dans les pays
anglo-saxons.
Les structures utilisées dans le programme
Nous allons créer un tableau comportant les nombres de un à dix-neuf, qui seront utilisés trois fois :
- pour tout nombre compris dans l’intervalle 1..19
- pour tout nombre compris dans l’intervalle 61..79
- pour tout nombre compris dans l’intervalle 81..99
A noter que parmi ces trois cas, seuls les nombres 61 et 71 se voient attribuer le mot « ET » entre le chiffre des dizaines et celui des unités.
On crée ensuite un tableau des dizaines qui contient les nombres vingt, trente, quarante, cinquante, soixante, soixante, quatre-vingt, quatre-vingt.
Remarque : 'soixante' et 'quatre-vingt' apparaissent deux fois, une fois en propre et l'autre pour former les cas spéciaux des intervalles 70..79 et 90..99.
On crée ensuite un tableau qui contient les unités restantes : mille, million, milliard,…
Nous allons supposer que le nombre saisi au clavier peut aussi contenir deux décimales.
Le principe récursif fait qu’on sait qu’un nombre à évaluer est égal à l’évaluation de sa partie principale (groupe de trois chiffres maximum) plus l’évaluation du reste
Exemple :
13.236.526,65
= évaluation de ’13’ + évaluation de ’236.526,65’
236.526,65 = évaluation de ’236’ +
évaluation de ’526,65’
526,65 = évaluation de ’526’ + ’virgule’
+ évaluation de ’65’
65 =
évaluation de ’60’ + évaluation de ’5’ =
’soixante’
+ ’cinq’ = ’soixante cinq’ ;
526 = évaluation de ’500’ + évaluation de ’26’
26 = évaluation
de ’20’ + évaluation de ’6’ = ’vingt’ + ’six’ = ’vingt six’
évaluation de ’500’ = ’cinq’ +
’cent’ = ’cinq cent’ ;
et ainsi de suite…
ensuite on n’a plus qu’à concaténer les résultats des différentes évaluations pour obtenir le résultat final.
La seule difficulté consiste à déterminer la partie principale d’un nombre. Nous avons en effet l'habitude de lire les nombres de gauche à droite en isolant les groupes de trois chiffres (millions, milliers) puis à l'intérieur les centaines, dizaines et unités. La seule difficulté pratique du langage consiste à déterminer le rang maximal du nombre, c'est-à-dire si le premier groupe à partir de la gauche est celui des milliards, millions, milliers , … mais pour cela, les yeux comptent les chiffres à partir de la droite !
Cette petite contradiction levée, l'algorithme que l'esprit suit intuitivement consiste à évaluer le groupe de trois chiffres le plus à gauche, puis à répéter l'opération en ne considérant que les chiffres restants à droite : cette méthode d'évaluation / séparation est caractéristique d'un processus récursif ! Seul point négatif, les résultats intermédiaires sont moins significatifs (voire même inexistants) que dans la méthode itérative et rendent difficile la gestion des exceptions du pluriel, etc …
Techniquement, l'algorithme va essayer de déterminer le groupe maximal à chaque étape et va analyser son coefficient, le traduire, puis relancer la fonction pour les chiffres restants : cela garantit qu'un groupe de trois chiffres tels que les millions ne seront évalués qu'une fois, car au prochain appel récursif un groupe de milliers (au plus) sera analysé , … , jusqu'à ce que l'on arrive finalement aux unités finales (ou des décimales) du nombre, terme de la récursivité.
Les
spécificités de l’algorithme
Avant
d'appeler la procédure récursive, on s'assurera tout d'abord que le nombre ne
contient pas une virgule, auquel cas on évaluera d’abord sa partie entière,
puis ensuite celle décimale (arrondie à deux décimales) ,
que l'on collera à la suite de la première et du mot « virgule » .
L'étape
de base consiste à récupérer la longueur du nombre, afin de prendre la partie
principale et l’évaluer. On fera ensuite un appel récursif et on collera cette
évaluation à l’évaluation du reste.
Nous avons créé un tableau contenant l’expression littérale des nombres de zéro à dix-neuf. Un nombre constitué d’un seul chiffre constitue le point terminal de la récursivité, et on renvoie tout simplement son équivalent en français.
Si le nombre reçu est compris dans les intervalles 10..99 , alors on considère que l’évaluation du nombre est égale au chiffre des dizaines plus l’évaluation (appel récursif) des unités. On distinguera ici les cas où on doit insérer un « ET » et les cas des dizaines « soixante-dix » et « quatre-vingt-dix ».
Si le nombre reçu est compris dans les intervalles 70..79 ou 90..99 alors l’évaluation est égale au chiffre des dizaines (lu dans le tableau) décrémenté de un plus l’évaluation (appel récursif) du chiffre des unités incrémenté de 10. On distinguera ici les cas où on doit insérer un « ET » .
Si le nombre reçu est compris dans l’intervalle 100..999 alors l’évaluation est égale au chiffre des centaines (exception faite du nombre 100) plus la chaîne « cent » plus une évaluation (appel récursif) du reste. On prendra en compte le cas du « s » final qui vient s’ajouter au « cent » dans certains cas.
Si le nombre est supérieur à 999 alors on détecte d’abord sa puissance de mille (mille, million, milliard…) qui constitue ce qu’on a appelé ci-dessus la partie principale, on l’évalue par un appel récursif (en lui collant ensuite la puissance de mille correspondante) et on lui concatène le reste qui est évalué par un appel récursif.
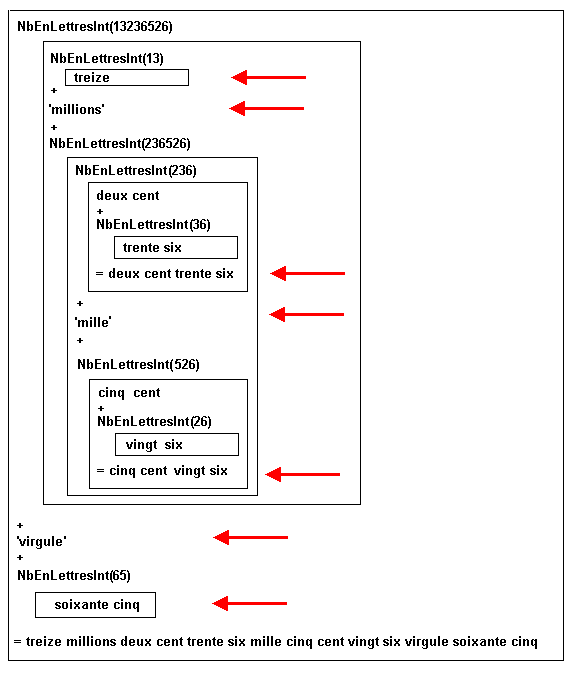
Voici un exemple des appels récursifs pour le nombre donné plus haut.