Le métro

Le programme suivant cherche le chemin le plus court pour aller d'une station de métro à une autre. Il fonctionne avec le métro parisien, mais il peut être bien évidemment être utilisé avec n'importe quel autre réseau.

Dans un premier temps, nous allons appliquer cet algorithme à un réseau très simple, avec quelques stations. C'est le programme qui suit. Le programme réel, avec toutes les stations du métro et les optimisations, est à télécharger.

Nous allons d'abord définir le type "arc", représentant le chemin entre deux stations; il contient le numéro de la station de départ, le numéro de la station d'arrivée et un indicateur qui nous dit si un arc a déjà été emprunté (afin d'éviter les boucles) :

arc = record
 depart, arrivee: integer;
 parcouru: boolean;
end;
 

Nous allons ensuite entrer les arcs correspondants :

procedure init_arcs;
begin
 t[1].depart := 1; t[1].arrivee := 2; t[1].parcouru := false;
 t[2].depart := 2; t[2].arrivee := 1; t[2].parcouru := false;
 t[3].depart := 2; t[3].arrivee := 3; t[3].parcouru := false;
 t[4].depart := 2; t[4].arrivee := 6; t[4].parcouru := false;
 t[5].depart := 2; t[5].arrivee := 11; t[5].parcouru := false;
 t[6].depart := 3; t[6].arrivee := 2; t[6].parcouru := false;
 t[7].depart := 3; t[7].arrivee := 4; t[7].parcouru := false;
 t[8].depart := 4; t[8].arrivee := 3; t[8].parcouru := false;
 t[9].depart := 6; t[9].arrivee := 4; t[9].parcouru := false;
 t[10].depart := 4; t[10].arrivee := 7; t[10].parcouru := false;
 t[11].depart := 4; t[11].arrivee := 9; t[11].parcouru := false;
 t[12].depart := 4; t[12].arrivee := 10; t[12].parcouru := false;
 t[13].depart := 5; t[13].arrivee := 6; t[13].parcouru := false;
 t[14].depart := 6; t[14].arrivee := 2; t[14].parcouru := false;
 t[15].depart := 6; t[15].arrivee := 4; t[15].parcouru := false;
 t[16].depart := 6; t[16].arrivee := 5; t[16].parcouru := false;
 t[17].depart := 6; t[17].arrivee := 9; t[17].parcouru := false;
 t[18].depart := 7; t[18].arrivee := 4; t[18].parcouru := false;
 t[19].depart := 8; t[19].arrivee := 9; t[19].parcouru := false;
 t[20].depart := 9; t[20].arrivee := 4; t[20].parcouru := false;
 t[21].depart := 9; t[21].arrivee := 6; t[21].parcouru := false;
 t[22].depart := 9; t[22].arrivee := 8; t[22].parcouru := false;
 t[23].depart := 10; t[23].arrivee := 4; t[23].parcouru := false;
 t[24].depart := 11; t[24].arrivee := 2; t[24].parcouru := false;
 min_stations := 10000; // initialisé à plus l'infini
end;
 

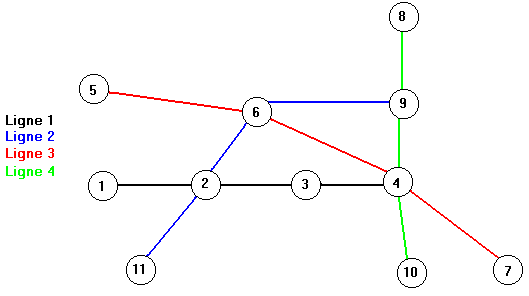
On doit faire ensuite une procédure qui pour un station donnée cherche toutes les stations qui sont à une distance de 1 de celle-ci. Ainsi, dans le dessin précédent, les stations situées à une distance de 1 de la station numéro 4 sont les suivantes: 3,6,9,7 et 10.

procedure trouve_partantes(depart: integer);
var i: integer;
begin
 nb_partantes := 0;
 for i := 1 to 24 do
 begin
 if t[i].depart = depart then
 begin
 inc(nb_partantes);
  partantes[nb_partantes] := i; // valeur de "i" utilisée dans "trouver"
 end;
 end;
end;
 

Ensuite, pendant le parcours du graphe (afin de chercher le chemin le plus court) si on a emprunté un arc, on doit le marquer; de cette façon, on empêche le programme de boucler. Inversement, si on a pris un chemin et qu'il s'est révélé infructueux, on doit faire demi-tour (en réalité on monte d'un niveau dans la pile de la procédure récursive) et marquer l'arc comme n'étant pas emprunté. Ce qui nous donne :

procedure marquer_arc(depart, arrivee: integer; marque: boolean);
var i: integer;
begin
 for i := 1 to 23 do
 begin
 if (t[i].depart = depart) and (t[i].arrivee = arrivee) then
 t[i].parcouru := marque;
 if (t[i].depart = arrivee) and (t[i].arrivee = depart) then
 t[i].parcouru := marque;
 end;
end;
 

Il nous reste maintenant à faire la fonction de recherche du plus court chemin entre deux stations. Cette fonction a les paramètres suivants :

- départ et arrivée, indiquant les numéros de stations

- nb_stations: variable indiquant (à un niveau n de la récursivité) le nombre de stations parcourues.

- liste: une chaîne de caractères, dans laquelle on mémorise les numéros des stations.

La programmation de cette fonction se fait de la manière suivante :

- pour chaque chemin trouvé, on mémorise le nombre de stations dans une variable, appelée "min_stations". De cette façon, on est sûr que la longueur des chemins trouvés va aller en diminuant.

- si on n'a pas trouvé le chemin (c'est à dire "départ<>arrivée") alors pour la station en cours (c'est à dire "départ") on mémorise toutes les stations partantes, et on les essaye une par une. Grâce à la récursivité, pour chacune de ces stations partantes on mémorise leur propres stations partantes et on les essaie (descente récursive et exploration de tous les chemins).

Il faut donc marquer l'arc emprunté, essayer la première station et si elle a échoué alors effacer l'arc emprunté et prendre la deuxième station; et ainsi de suite.

function trouver(depart, arrivee, nb_stations: integer; liste: string): boolean;
var i: integer;
 partantes1: tp;
 nb_partantes1: integer;
begin
 if depart = arrivee then
 begin
 trouver := true;
 if nb_stations <= min_stations then
 begin
 min_stations := nb_stations;
 form1.memo1.lines.add('Nouveau plus petit chemin :');
 form1.memo1.lines.add(inttostr(nb_stations) + ' stations.');
 form1.memo1.lines.add(liste);
 form1.memo1.lines.add('=============================');
 end;
 end
 else
 begin
 trouve_partantes(depart);
 move(partantes, partantes1, sizeof(tp));
 nb_partantes1 := nb_partantes;
 for i := 1 to nb_partantes1 do
 if t[partantes1[i]].parcouru = false then
 begin
 marquer_arc(depart, t[partantes1[i]].arrivee, true);
 trouver := trouver(t[partantes1[i]].arrivee, arrivee,
 nb_stations + 1, liste + ',' + inttostr(t[partantes1[i]].arrivee));
 marquer_arc(t[partantes1[i]].arrivee, depart, false);
 end;
 end;
end;
 

On n'a plus qu'à appeler la fonction ci-dessus :

procedure TForm1.Button1Click(Sender: TObject);
begin
 init_arcs;
 trouver(5, // station départ
 7, // station arrivée
 0, // stations parcourues
 '5'); // chemin parcouru
end;
 

Passons maintenant dans le cas réel, c'est à dire environ 300 stations de métro.

Là, prendre tous les chemins peut s'avérer extrêmement long. C'est pour cette raison qu'on introduit un nombre maximal de changements autorisés.

L'algorithme prend les chemins dans l'ordre de leur introduction en mémoire. Si on lui laisse un nombre maximal de 5 changements par exemple, alors le nombre de chemins possibles sera beaucoup plus grand que si on lui impose seulement 2 changements. C'est donc à vous de choisir et de faire des essais, pour déterminer le trajet et le temps de trajet qui vous convient le mieux.

Le programme fonctionnel des stations de métro est à télécharger.

On peut ensuite modifier l'algorithme de recherche en ne lui donnant que les stations qui se trouvent à un croisement, de cette façon la recherche sera encore plus rapide. Actuellement le programme met de 1 seconde à quelques minutes pour trouver un chemin optimal, mais l’affichage des solutions est progressif.

Télécharger le code source Delphi