Le parcours du fou
Nous avons un échiquier et un fou situé dans un coin noir. Il faut faire arriver ce dernier dans le coin opposé, en le faisant passer une seule fois sur une case, dans le même sens de déplacement. Cela signifie que le fou ne peut pas passer deux fois par la même case en ayant le même sens de déplacement.
exemple : un
fou a deux sens de déplacement. On décide que le premier sens, nommé A, et le
deuxième sens, nommé B, sont indiqués sur les dessins suivants :
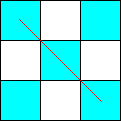
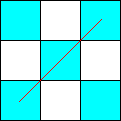
sens A sens B
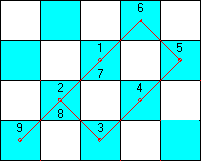
Ainsi, le parcours correspondant à l'image ci-dessous n'est pas possible, car le fou parcourt les cases 1,2,3,4,5,6 sans problème, mais ensuite il va de 7 (numéroté aussi 1) en 8 (numéroté aussi 2) dans le sens B (défini ci-dessus). Or, la case 1 avait déjà été visitée dans le sens B, pour aller dans la case 2. De même, le fou ne peut aller de la case 9 à la case 6 en passant par les cases 2 et 1, car ces deux cases ont déjà été visitées dans le sens B.
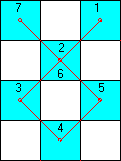
En revanche, le parcours correspondant au dessin suivant est possible, car le fou parcourt les cases 1,2,3 dans le sens B. Ensuite, une fois arrivé en 5 il passe à nouveau dans la case 2 (numérotée aussi 6), mais cette fois-ci dans le sens A. Une fois en 6, il ne pourra aller qu'en 7 car les cases 1 et 3 ont déjà été parcourues dans le sens B, et la case 5 a déjà été parcourue dans le sens A quand on est allé de 5 vers 6.
Nous allons créer l'algorithme de ce programme. On a un échiquier dont chaque case est associée à deux sens. Pour savoir si toutes les cases ont été parcourues, on ne peut pas compter le nombre de sauts, car on ne sait pas combien il y en a. En effet, le fou peut passer 2 fois sur une même case, et ceci pour n cases. Nous devons donc associer aussi aux cases une valeur booléenne, dont le rôle sera d'indiquer qu'elle a été visitée ou non. Si toutes les cases noires ont été visitées, alors on obtient un total de 32. Pendant le parcours, on doit mémoriser les numéros des cases parcourues, et, comme une case peut être visitée au maximum 2 fois, on a prévu un tableau de mémorisation dont la taille est égale au double du nombre de cases noires. Il est vrai que le fou ne peut aller dans les coins qu'une fois, donc il faudrait enlever 2 au résultat, mais le fait d'ajouter 2 éléments au tableau n'est pas un lourd handicap.
exemple :
pour un échiquier de 8*8 cases, il y a (8*8)/2 = 32 cases noires. Le nombre de
coups théorique est de 32*2 (passage 2 fois dans chaque case) moins 2 (les
coins), soit 62.
Structures des données
const lim1 = 8;
lim2 = 8;
type case_ec = record
sensA, sensB, visite: boolean; end;echiquier = array[1..lim1, 1..lim2] of case_ec;
var ech: echiquier; //--- echiquier des coups joués
coups: array[1..lim1 * lim2] of integer; //--- liste des coups mémorisés
On écrit ensuite la fonction qui vérifie que toutes les cases ont été visitées:
function tout_a_ete_visite: boolean;
var i, j, total: integer;
begin
total := 0;
for i := 1 to lim1 do
for j := 1 to lim2 do
if ech[i, j].visite then inc(total);tout_a_ete_visite := (total = (lim1 * lim2 div 2));
end;
La procédure qui simule le parcours du fou est bien entendu récursive. Elle a trois paramètres :
- x1 et y1 sont les coordonnées du fou au coup précédent
- coup : numéro du coup, utilisé pour mémoriser les déplacements du fou
Nous avons décidé d'arrêter l'algorithme après le premier parcours trouvé, mais rien ne vous empêche de supprimer le test sur la variable fini, pour laisser le programme chercher toutes les solutions.
Voyons le coeur du programme : on a quatre directions possibles, représentées par les tableaux dx et dy. A partir de chaque case, on essaye d'aller dans chacune des quatre directions, ce qui nous amène à l'utilisation d'une boucle for i:=1 to 4 do. On calcule ensuite les coordonnées de la prochaîne case, en utilisant les tableaux dx et dy : new_x:=x1+dx[i]; new_y:=y1+dy[i]; et on s'assure que cette case est bien sur l'échiquier. Suivant la valeur de i, on se trouve ou bien dans le sens A, ou bien dans le sens B. Supposons que nous sommes dans le sens A. Comme on va se déplacer dans une autre case, il faut sauvegarder les paramètres de la case en cours, marquer son sens A, marquer le sens A de la case où on va sauter (de cette façon, si on y repasse au bout de n sauts, on ne pourra pas utiliser le sens A), faire un appel récursif avec les coordonnées de la nouvelle case, et quand on sort de la récursion, restaurer les valeurs telles qu'elles étaient avant le saut. Il ne faut évidemment pas oublier de positionner à true le booléen visite de chaque case qui a été visitée au moins une fois.
Le même ensemble d'instructions s'applique pour le sens B; nous obtenons le programme suivant :
procedure chemin(x1, y1, coup: integer);
const dx: array[1..4] of integer = (1, 1, -1, -1); //--- 1 et 3 : sens 1
dy: array[1..4] of integer = (1, -1, -1, 1); //--- 2 et 4 : sens 2
var i, new_x, new_y: integer;
old_s11, old_s12, old_s21, old_s22, visit: boolean;begin
coups[coup] := y1 * 10 + x1;
if tout_a_ete_visite then
begin
max_coups := coup;fini := true;
end else beginfor i := 1 to 4 do
begin new_x := x1 + dx[i]; new_y := y1 + dy[i]; if not fini thenif (new_x >= 1) and (new_x <= lim1) and
(new_y >= 1) and (new_y <= lim2) then
if (i mod 2) = 1 then
begin if not ech[new_x, new_y].sensA thenbegin
//--- sauvegarde anciennes valeurs
old_s11 := ech[new_x, new_y].sensA;
old_s12 := ech[x1, y1].sensA; //--- sauvegarde sensA
visit := ech[new_x, new_y].visite;//--- modifications
ech[new_x, new_y].sensA := true; ech[new_x, new_y].visite := true;ech[x1, y1].sensA := true; //--- modif sensA
//--- appel récursif
chemin(new_x, new_y, coup + 1);
//--- restauration anciennes valeurs
ech[x1, y1].sensA := old_s12; //--- restaure sensA
ech[new_x, new_y].sensA := old_s11; ech[new_x, new_y].visite := visit; end; end else begin if not ech[new_x, new_y].sensB thenbegin
//--- sauvegarde anciennes valeurs
old_s21 := ech[new_x, new_y].sensB;
old_s22 := ech[x1, y1].sensB; visit := ech[new_x, new_y].visite;//--- modifications
ech[new_x, new_y].sensB := true; ech[new_x, new_y].visite := true; ech[x1, y1].sensB := true;//--- appel récursif
chemin(new_x, new_y, coup + 1);
//--- restauration anciennes valeurs
ech[x1, y1].sensB := old_s22; ech[new_x, new_y].sensB := old_s21; ech[new_x, new_y].visite := visit; end; end; end;end;
end;
Télécharger le code source Delphi